曲线的拟合优度

当用拟合的曲线回归方程描述两变量间的曲线关系时，经常需要回答两个问题：一是拟合的曲线有无意义，即此曲线关系能否成立； 二是拟合的效果如何。如果曲线拟合是利用直线化的原理来完成的，那么，回答第一个问题可用直线化方程的假设检验，即直线化方程成立，则曲线关系也成立，反之亦然；回答第二个问题可用直线化方程的拟合效果检验，意即直线化方程拟合是好的，则曲线拟合也是好的，反之亦然。这两种检验方法通称为曲线的拟合优度检验，均用方差分析。
直线化方程的假设检验 参见条目“直线回归”中“直线回归方程的假设检验”。这里只需用直线化方程中变换后的变量x、y代替直线方程中的变量X、Y就行了。如例1中用x=lgX代X，用y=lg(Y+10)代Y。
例1 在条目 “双曲线拟合”的例1中，用最小二乘法求得压力(mmHg)X与二酰肼生存率(%)Y的直线化方程为ŷ=2.2238-0.3862x，式中x=lgX,y=lg(Y+10)。试由此推断lg(Ŷ+10) = 2.2238-0.3862 lgX的曲线关系能否成立？ (提示： 前已算得lxx=2.0323,lxy=-0.7848)。
H₀: 总体回归系数β=0,
H₁: β≠0。a=0.05。
由条目 “双曲线拟合”表1算得n=6,Σy=8.8207,Σy²＝13.2728。

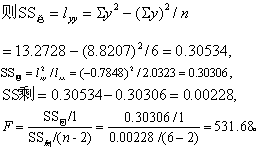
今v1 =1,v2=6-2=4，查F界值表得P<0.01，按a=0.05水准拒绝H₀，接近H₁，可认为x、y间有直线关系，即上述曲线关系能成立。
直线化方程的拟合效果检验 对直线回归方程作假设检验，得P≤a，只能说明因素X的一次项对指标Y的影响是不可忽视的。如果除X的影响外，还有其他未加控制的、不可忽视的影响因素，则此直线的拟合效果就不能算是好的，称为失拟。要判断直线拟合效果的好坏需做一些重复试验。比如例2中将五种稀释液Xi各重复了10次，共得50个观察值Y_ij，并作变换：x=lgx,y_ij＝lg(Y_ij-4)。可以证明，在各试验点Xi处，重复次数相等的情况下，如例2，在用x及其对应的10个y_ij的均数y(共5个数对)，按最小二乘法求得直线方程与分别用每个x及其对应的10个y_ij值(共50个数对)求得的直线方程完全一样。据此，可按下述步骤检验直线化方程的拟合效果。检验假设H0为失拟均方等于误差均方，H₁为两个均方不等。
(1)按式(2)求y变异的总离均差平方和SS_总、回归平方和SS_回、失拟平方和SS_失、误差平方和SS_误及其相应的自由度v。数理统计证明：
SS_总＝SS_回+SS_失+SS_误。(1)

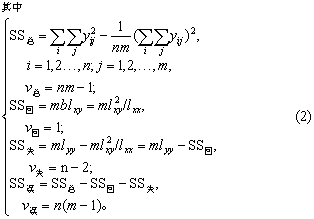
式中n为对子数(只计x的取值个数),m为重复次数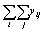，为y_ij的所有重复观察值之和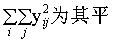，方和。其余符号同前。
(2)将式(2)计算结果列方差分析表，如表2；再按式(3)计算统计量F₁值，

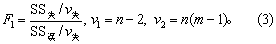
查F界值表得P值，按所取检验水准α作出推断结论：若P≤α，则拒绝H₀，接受H₁，说明SS失中除含有误差的影响外，还有其他因素的影响，需进一步查明；若P>α，则不拒绝H₀，说明SS_失基本上可看成是误差等偶然因素引起的。这时继续下一步。
(3)将SS_失与SS_误合并，其相应的自由度亦合并，按式(4)计算统计量F₂值，作直线化方程的假设检验(H₀为β=0)。

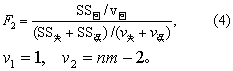
查F界值表得P值，若结论为拒绝H₀，说明回归方程的拟合效果较好；若不拒绝H₀，说明引入x的一次项没有多大作用，即此直线所对应的曲线关系不成立。
注意： 非重复试验时，直线化方程的假设检验中的F检验，与重复试验时的F₂检验不同，后者的误差自由度要大得多。
例2 为测定人体免疫球蛋白G的含量，拟制备标准血清稀释度倍数X与沉淀环直径(mm)Y的标准曲线。每种稀释度各重复10次，资料见表1。已拟合曲线的直线化方程为lg(Y-4)=1.6975-0.8664 lgX，问拟合的效果如何？(提示： 已得lxx=0.6938,lyy=0.5243,lxy=-0.6011)。
H₀: 失拟均方等于误差均方，
H₁:失拟均方不等于误差均方。
α=0.05。
今n=5,m=10。对表中50个Y_ij值作y_ij＝lg(Y_ij-4)变

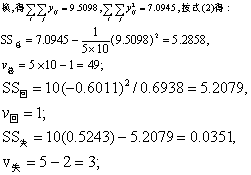
表1 五种稀释度X各重复测10次沉淀环直径Y

X x	20 1.3010	25 1.3979	50 1.6990	100 2.0000	200 2.3010
Yij	8.0 7.8 7.8 8.0 8.2 7.8 8.0 7.5 8.0 8.0	7.2 7.0 7.2 7.0 7.2 6.9 7.0 7.1 6.8 6.8	5.5 5.8 5.5 5.7 5.5 5.5 5.6 5.4 5.3 5.5	5.0 5.0 5.0 4.9 5.0 5.0 5.1 5.0 5.0 5.0	4.5 4.6 4.5 4.5 4.5 4.4 4.5 4.5 4.5 4.5
y（均数）	0.5917	0.4795	0.1830	-0.0004	-0.3028

表2 拟合效果的方差分析

变异来源	v	SS	MS	F
总	49	5.2858
回归 失拟 误差	1 3 45	5.2079 0.0351 0.0428	5.2079 0.0117 0.00095	5482.00(F回) 12.32(F1)

SS_误＝5.2858-5.2079-0.0351=0.0428,
v_误＝5(10-1)=45。
以F₁查F界值表得P<0.01，按α=0.05水准拒绝H₀，接受H1，说明SS_失中除误差的影响外，尚有其他因素的影响，待进一步查明。但F回有显著性(P<0.01)，说明x的一次项对y有一定作用，但直线的拟合尚不够好，即此曲线拟合的效果尚不够好。