普遍二次曲面的主方向
普遍二次曲面的主方向pubian erci qumian de zhu-fangxiang
若一个普遍二次曲面的径平面垂直于所平分的弦,则叫做主平面. 一个二次曲面至少有一个确定的主平面,最多有三个主平面,每两个主平面的交线叫做主轴. 一个二次曲面最多有三个主轴. 设普遍二次曲面的方程为: F (x,y,z) ≡ax2+ by2+ cz2+2fyz+2gzx+2hxy+2ux+2vy+2wz+d=0 (a2+b2+c2+f2+y2+h2≠0),方程K3-K2 (a+b+c) +K (A+B+C)—I3=0,叫做F (x,y,z)=0的特征方程,它的根叫做特征根.式中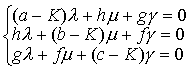 A,B,C分别是I3中a,b,c的代数余子式. 对于特征根K,以方程组:
A,B,C分别是I3中a,b,c的代数余子式. 对于特征根K,以方程组:
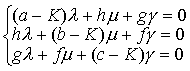
☚ 普遍二次曲面的中心 普遍二次曲面不变量的完全系统 ☛
- 谤书一箧是什么意思
- 谤书满箧是什么意思
- 谤书盈箧是什么意思
- 谤书诬是什么意思
- 谤从誉生是什么意思
- 谤伤是什么意思
- 谤僧骂道是什么意思
- 谤刺是什么意思
- 谤勃是什么意思
- 谤口是什么意思
- 谤咎是什么意思
- 谤喙是什么意思
- 谤嗤是什么意思
- 谤嘲是什么意思
- 谤国是什么意思
- 谤声是什么意思
- 谤嫉是什么意思
- 谤帖是什么意思
- 谤弃是什么意思
- 谤忌是什么意思
- 谤怒是什么意思
- 谤怨是什么意思
- 谤成市虎是什么意思
- 谤政是什么意思
- 谤木是什么意思
- 谤来不戚,誉至不喜是什么意思
- 谤架是什么意思
- 谤毁是什么意思
- 谤毫末者, 不见天地之大; 审小音者, 不闻雷霆之声。是什么意思
- 谤沮是什么意思
- 谤消金是什么意思
- 谤焰是什么意思
- 谤玉是什么意思
- 谤端是什么意思
- 谤箧是什么意思
- 谤累是什么意思
- 谤缺是什么意思
- 谤臣诬是什么意思
- 谤言是什么意思
- 谤言三至是什么意思
- 谤訾是什么意思
- 谤讟是什么意思
- 谤讥是什么意思
- 谤讦是什么意思
- 谤讪是什么意思
- 谤议是什么意思
- 谤议汹汹是什么意思
- 谤议沸腾是什么意思
- 谤论是什么意思
- 谤诅是什么意思
- 谤词是什么意思
- 谤诬是什么意思
- 谤语是什么意思
- 谤诮是什么意思
- 谤说是什么意思
- 谤诽是什么意思
- 谤谗是什么意思
- 谤起营蝇是什么意思
- 谤辱是什么意思
- 谤铄是什么意思