中心矩

---

指随机变量(x)对平均数(μ)的离差(x－μ)的k阶矩。

它的应用很广，常用μ_k表示。对离散型随机变量的k阶中心矩的一般公式为：

μ_k=E［(x－μ)^k］

=∑(x₁－μ)^kf(x₁)

对连续型随机变量的k阶中心矩为：

μ_k=E［(x₁－μ)^k］

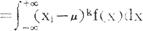
一阶中心矩恒等于零，二阶中心矩即方差(σ²)。

如果随机变量的分布对称于数学期望E(X)，则它的所有奇数阶中心矩都等于零，故任意奇数阶中心矩可作为描述分布的非对称性的特征。通常利用三阶中心矩(μ₃)表示分布的偏斜程度，除以σ³，消除单位影响，用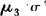作为偏度。μ₃／σ³＞0，分布为右偏；μ₃／σ³＜0，分布为左偏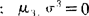，分布为对称。四阶中心矩(μ₄)常用来描述分布的峰度高低的度量，并用μ₄／σ⁴表示峰度的高低，当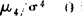称高峰态；μ₄／σ⁴＜0称低峰态。正态分布的偏度和峰度都等于零。

对随机变量的统计分布，类似的有相应的统计中心矩，其计算公式相仿，如k阶统计中心矩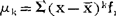₁，f₁为频率。