时间序列Time Series

将某一现象发生的数量变化，依时间的先后顺序排列形成的序列。用以预测现象发展的方向及其数量。

时间序列

社会、经济、自然现象的数量指标依时间顺序排列起来的统计数据。时间序列分析是一种动态数列的分析，目的在于掌握统计数据依时间变化的规律。时间序列分析一般可以分成以下四种情况：(1) 长期趋势分析。一些现象随时间变化而表现出某种趋向，它按某种规则增长或下降，或维持在一定水平上。长期趋势分析就是分析该现象随时间变化而呈现出的某种趋势性的变化规律。(2) 季节性变动分析。一些现象在春、夏、秋、冬四季变化中表现出某种规律性变化，存在着淡季与旺季。季节性变动分析就是分析该现象随着季节的变动而表现出的某种变化规律。(3) 循环变动分析。某些现象会依照一定的周期而呈现出一种循环性的变动。循环变动分析就是研究这种周期性循环变动的规律。(4) 不规则变动分析。一些现象的变化是由许多不可控制的原因引起的。这种变化没有规则，难以预料。不规则变动分析就是研究这种不规则变化的规律。

时间序列time series

依时间变动而顺序排列的一列数字。时间序列实际就是随机过程的一个“实现”或“观测”。

时间序列

按某种（相等或不相等的）时间间隔，对客观事物进行动态观察，由于随机因素的影响，各次观察的指标X₁,X₂,X₃，…，X_i，…都是随机变量，这种按时间顺序排列的随机变量的一组实测值称为时间序列。例如自动监测仪器描记的结果，病例随访资料，以及发病率、病死率、出生率、死亡率等指标的定期观测数据都是时间序列。分析时间序列，可以从运动中深入认识事物的本质(如几个时间序列间有无差别，一个较长的时间序列有无周期性等)，或对未来情况进行预测预报。
分析时间序列的方法很多，随数据的性质和分析的目的而异，一般都比较繁琐，往往涉及较深的数学知识，多半要借助于电子计算机。对时间序列的深入研究属于概率论的重要分支——随机过程的范畴。本条目仅就几个常见问题的分析方法作一简介。
(1)两个或多个时间序列差别的假设检验： 对于近似正态分布的序列，例如比较两组或几组儿童生长发育的动态观察数据，可将每个时间间隔上的观察值或其增长量当作一个指标，按多元假设检验或多元方差分析去处理。
(2)两组或多组病例随访资料的生存期（或缓解期）比较：见条目“病例随访资料分析”。
(3)周期性检验： 为了深入地分析一个较长的时间序列，往往需要检查其周期性的有无和长短(有时，一个复杂的时间序列还可以看成是几个长短不同的周期性因素综合作用的结果)。此时，可以利用图解法和方差分析来处理。
例 有长度n为20的时间序列： 3.7,4.0,11.5,7.5,3.8,3.0,6.6,7.7,5.9,2.0,4.4,4.9,7.2,9.4,4.1,3.2,7.8,10.9,5.8,6.0。问此序列有无周期性及周期性的长短如何？
以时间t为横坐标，观察值为纵坐标，作图如下。从图中可以

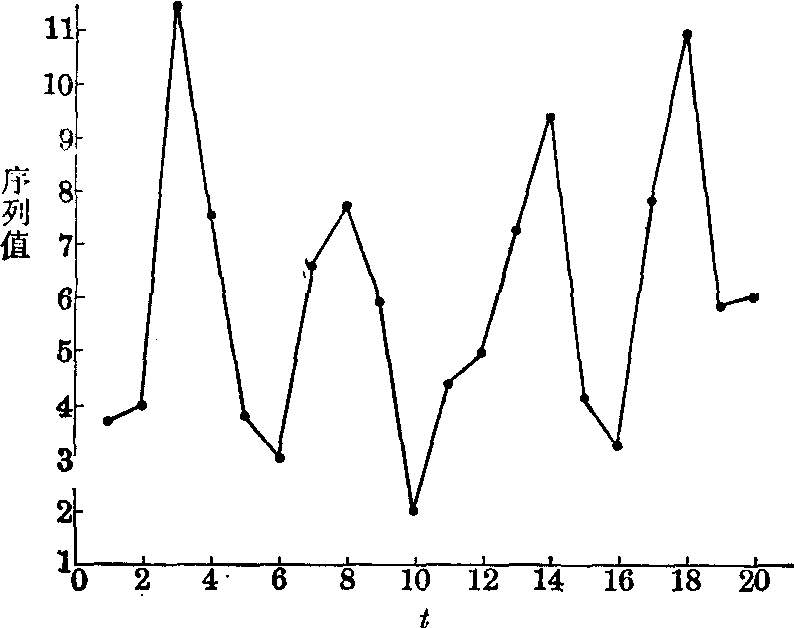
本例资料图示

直观地看出：此时间序列有周期性，有4个峰，故周期数为4，周期长度为20/4=5。现进一步将数据按此周期长度排列成表1，再作方差分析(见表2)。

表1 本例数据排成5列

列号	1	2	3	4	5
合计	3.7 3.0 4.4 3.2	4.0 6.6 4.9 7.8	11.5 7.7 7.2 10.9	7.5 5.9 9.4 5.8	3.8 2.0 4.1 6.0
	14.3	23.3	37.3	28.6	15.9

H₀:列间各总体均数相等，即此时间序列无周期性，
H₁:列间各总体均数不等，即此时间序列有周期性。
α=0.05。

表2 表1资料的方差分析

		SS	v	MS	F
总 列 列	间 内	130.38	19
		89.54 40.84	4 15	22.38 2.72	8.22

查F界值表得P<0.01，按α=0.05水准拒绝H0，接受H1，故可认为上述序列有长度为5的周期性。
(4)预测预报： 有一种时间和状态指标都是离散型的时间序列，其特点是无后效性，即假定要预报的结果只和紧前面的状态指标有关，而与以往的历史状态无关，也就是只和现状（最近的观察结果）有关，这种时间序列称为Markov链。连续型指标也可以离散化后再用Markov链处理，只要基本上符合无后效性的假定便可。例如根据Markov链的一个重要性质： k阶转移概率矩阵是一阶转移概率矩阵的k次方，便可由此求得某病由i型转到j型的概率。如有人对慢性肾病患者的肾功能作了长期随访(共计459人年)，患者的肾功能按酚红(PSP)排泄试验结果分为五类：PSP≥35%为第1类，25～34%为第2类，15～24%为第3类，5～14%为第4类，≤4%为第5类。以大样本的频率作为概率的近似值，得一年转移概率（矩阵）见表3。如第1行第1列的数值0.730，表示第1类患者1年后仍为第1类的概率是0.730，它是根据观察200例第1类患者1年之后有146例仍为第1类而算出的频率，即146/200=0.730；余类推。

表3 五类慢性肾病患者的一年转移概率

类别	1	2	3	4	5	合计
1 2 3 4 5	0.730 0.313 0.021 0.000 0.000	0.255 0.497 0.167 0.038 0.000	0.015 0.184 0.645 0.115 0.000	0.000 0.006 0.167 0.385 0.000	0.000 0.000 0.000 0.462 1.000	1.000 1.000 1.000 1.000 1.000

从表3可以看出： 第1类病人，1年后有27%(=25.5%+1.5%)转变为第2类和第3类而不致于直接转变为第4类和第5类；第3类病人，1年后有64.5%基本上维持原状，其余病人好转与恶化的大致各半，前者略多于后者；第4类病人有46.2% 1年后转为5类；第5类病人没有好转的希望，等等。慢性肾病患者2年转移概率矩阵，可由表3概率矩阵自乘求得(见表4)；慢性肾病患者3年转移概率矩阵，可由表3概率矩阵乘表4概率矩阵求得(见表5)。

表4 慢性肾病患者二年转移概率

类别	1	2	3	4	5	合计
1 2 3 4 5	0.613 0.388 0.081 0.014 0.000	0.315 0.357 0.203 0.053 0.000	0.068 0.216 0.466 0.125 0.000	0.004 0.036 0.173 0.168 0.000	0.000 0.003 0.077 0.640 1.000	1.000 1.000 1.000 1.000 1.000

表5 慢性肾病患者三年转移概率

类别	1	2	3	4	5	合计
1 2 3 4 5	0.548 0.400 0.132 0.029 0.000	0.324 0.314 0.206 0.057 0.000	0.112 0.215 0.359 0.110 0.000	0.015 0.052 0.146 0.086 0.000	0.002 0.019 0.157 0.717 1.000	1.001 1.000 1.000 0.999 1.000

从表5可以看出：第1至4类病人3年后转变为5类的各有0.2%,1.9%,15.7%和71.7%；将表5与表3、表4比较，还可看出第2至4类病人经3年好转为1类的概率比经1年或2年转变为1类的概率更大等等。

时间序列

又称时间数列或动态数列。是按照时间的先后顺序排列的一系列观测值。其由两部分组成： (1) 现象所属的时间，有年份、季度、月份或其他任何时间形式； (2) 现象在不同时间上的观测值，其表现形式有绝对数、相对数、平均数。

时间序列time series

也称时间数列。是指将表明社会经济现象的某种数量指标的数值，按时间先后顺序排列而成的数列。时间序列通常按离散形式记录，如某产品的月销售量、某国的年国民生产总值、某股票的每天收盘价等等。时间序列可分为确定性时间序列和随机性时间序列。时间序列的编制原则是：时间序列的时期间隔应相等；总体范围应统一，即地区范围、隶属关系范围、分组范围等应统一；指标的经济内容、计量方法、计量单位与计算价格等也应统一。如不统一，则应采取相应的办法进行调整与核算。编制和研究时间序列的目的在于研究社会经济发展的过程、趋势和规律等。但在时间序列中，每个时期数值的大小都受许多不同因素的影响，例如，某商品月销售量除受居民购买力的影响外，还受商品的价格、季节的变化、居民的偏好程度等因素的影响。若要详细测量各种因素的影响程度将是相当困难的。因此，需要对时间序列进行分析。时间序列分析主要包括：
❶时间序列因素分析即长期趋势、季节趋势、循环变动和不规则变动。其中长期趋势反映了事物的主要变化趋势。
❷时间序列的组合形式是：加法型、乘法型与混合型。
时间序列分析的最基本理论基础是40年代 分 别 由 Norbort Wiener 和 Andrei Kolmogonor独立提出的，他们对发展时间序列的参数模型拟合和推断过程作出了贡献。70年代的G.P.Box和G.M.Jenkins发表的专著《时间序列分析：预测和控制》，提出了自回归滑动平均模型，从而提供了传统计量经济学和时间序列技术的综合基础，又经Hendry等人提出的“一般到特殊”的建模方法、协整分析等，进一步将时间序列与计量经济方法有效地结合。