方差分析analysis of variance

将包含k个样本(一般k≥3)的试验观察值总变异的平方和与自由度分解为不同变异来源的平方和与自由度，求得各变异来源的总体方差估值，计算适当的F值以测验各样本是否具有相同的总体均值。即测验H₀:μ₁＝μ₂＝…=μk=μ，或记作μi=μ(i=1,2，…，k)是否成立的统计推断方法。对于不同设计的试验资料应采用不同的方差分析方法。这里介绍两种最基本的方差分析方法。
单向分组资料的方差分析 研究一个因素A的不同水平对所考察对象的影响，A取k个水平A_i(其分

❸给出显著水平a。

❹由F分布查自由度为k-1,n-k的F分布上a分位数Fa。

❺列统计量计算表(表1)。

❻列方差分析表(表2)。

表1 单向分组资料方差分析统计量计算表

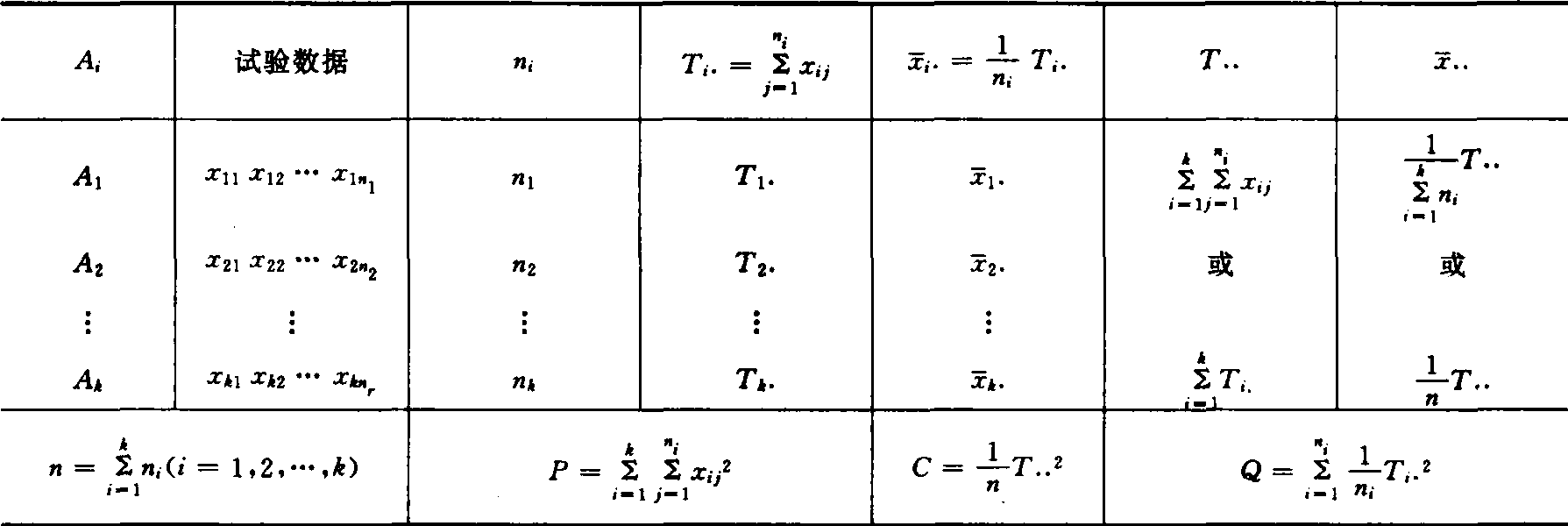
表2 单向分组资料方差分析表

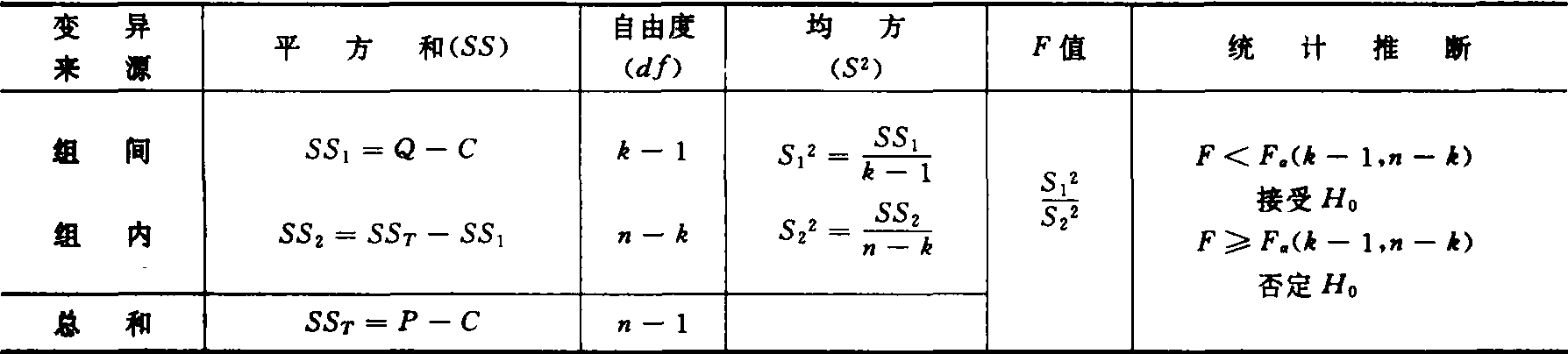
双向分组资料的方差分析 单因素完全随机区组设计试验（参见随机区组设计）中，区组看作一个试验因素，若试验因素A取k个水平，区组数（重复数）为n则所得试验数据{x_ij}(i=1,2，…，k;j=1,2，…，n)符合k行，n列双向分组资料模式(如表3)。检验因素A的效应或区组效应对试验结果有无显著影响，其步骤如下：
❶假设H₀,A因素效应对试验结果无显著影响，即μ_i＝μ(i=1,2，…，k)或区组效应对试验结果无显著影响，即μ_j＝μ(j=1,2，…，n)。

❷确定统计量并明确其分布

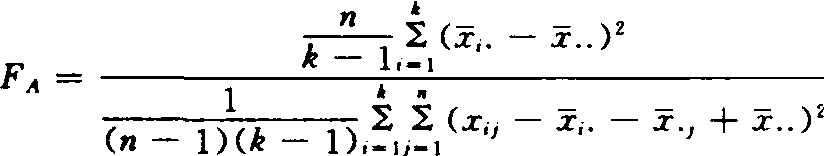
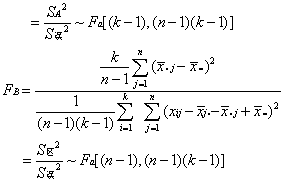
❸给出显著水平α

❹查F表得Fa[(k-1,(n-1)(k-1)]和Fa[(n-1),(n-1)(k-1)]值

❺列表计算统计量(表3)

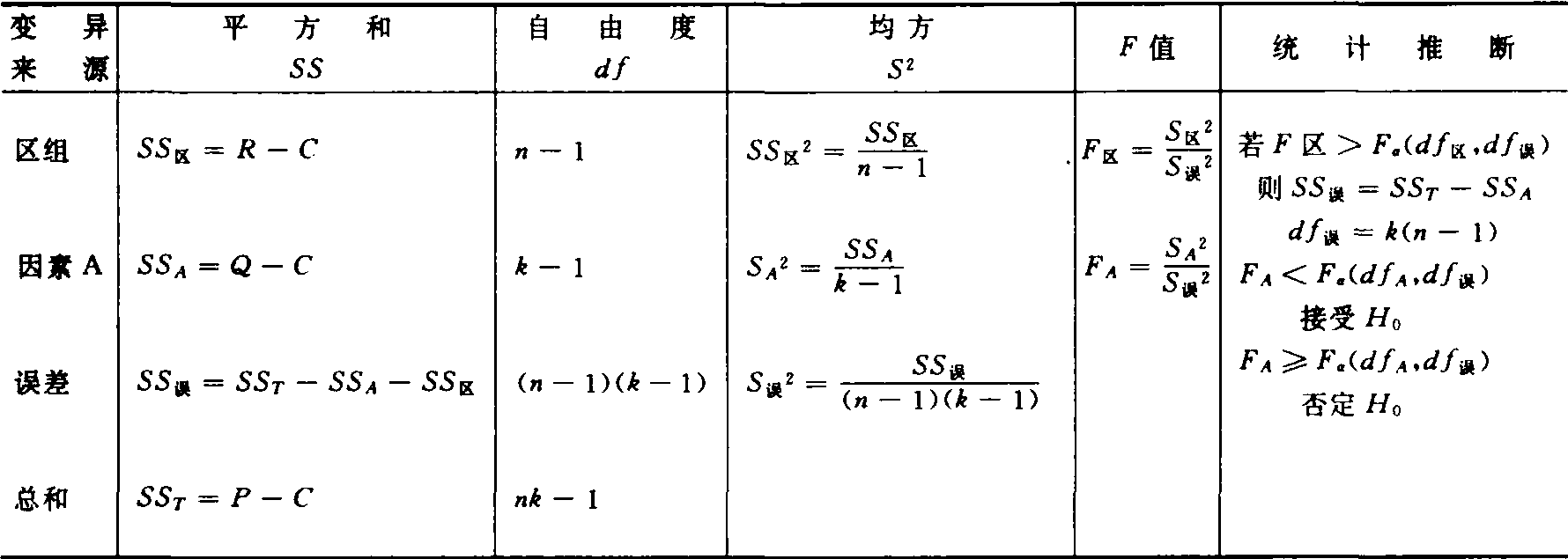
❻列方差分析表(表4)

表3 双向分组资料方差分析统计量计算表

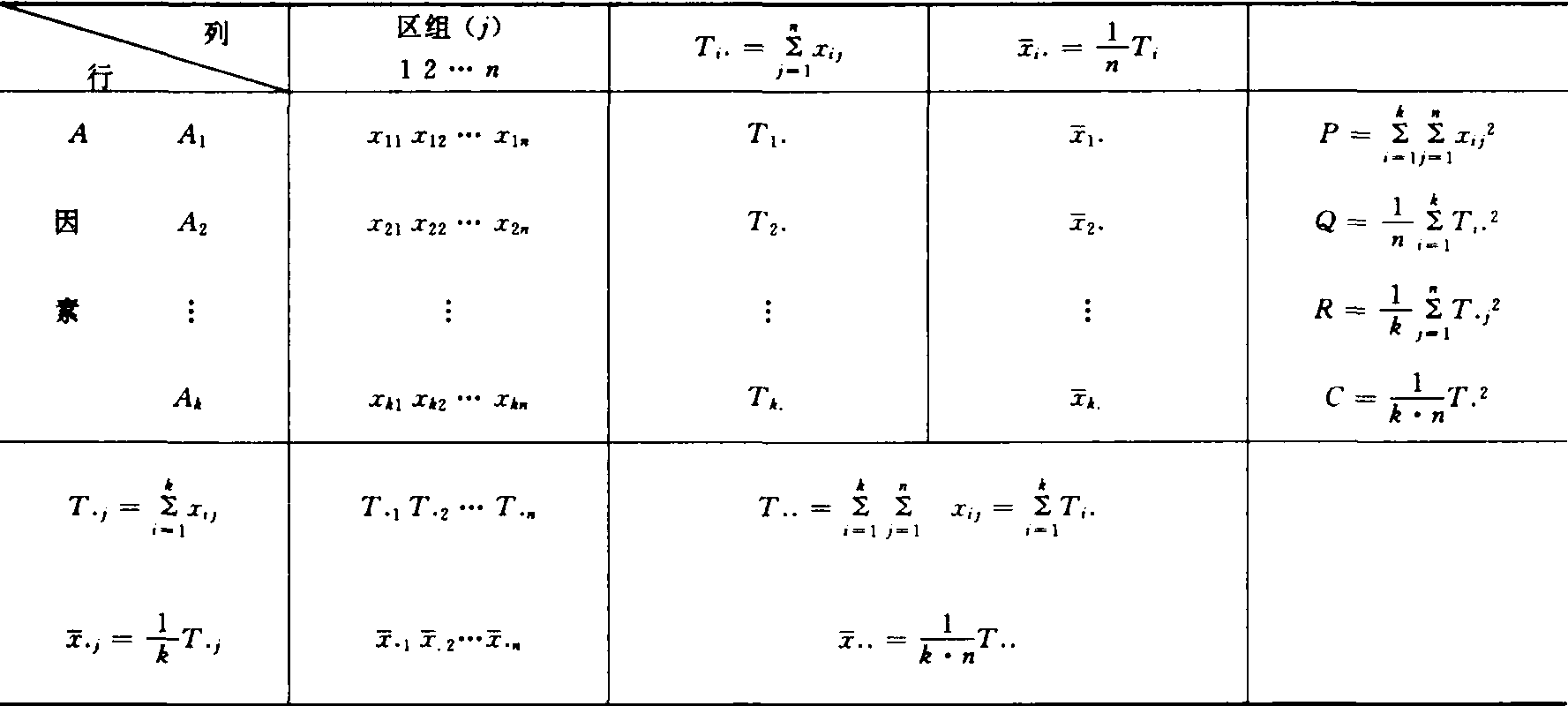
表4 双向分组资料方差分析表

方差分析

分析检验数据的一类统计方法。假定观察值为各因子效应的代数和，则在互相正交的前提下，观察值对其平均的偏差的平方和再加上误差的平方和，总自由度可写成各因子自由度的代数和，通过比较某一因子的均方和误差的均方来推知因子对于观察结果有无显著影响，按因素个数的多少，分为单因素分析和多因素分析。常被应用于测验分数统计中。

方差分析variance analysis

旧译变异量分析。统计分析上，进行多个样本平均数假设测验的一种方法。方差是平方和除以自由度所得的商，也是标准差的平方，常用s²表示。将观察值总变异的自由度和平方和分解为各项变异来源的自由度和平方和，并计得相应的方差（均方），进而进行F测验以判断各处理项的差异显著性。如果F测验表现显著，则进行各处理平均数数的多重比较。由于数学模型的不同，方差分析还包含更为广泛的内容。

方差分析fangcha fenxi

指教育实验中分析数据的一种基本方法。进行教育实验所取得的数据都包含着两种变差：
❶条件变差。是由实验处理或实验条件不同而造成的差异；
❷随机变差。是由实验处理或实验条件之外的随机因素所造成的差异。方差分析的目的就是设法把这两种变差分开，进而加以比较。如果条件变差（亦称组间变差）比随机变差（亦称组内变差）大，就说明处理或条件重要而不可忽视；如果它们之间相差较小，则说明处理或条件并不重要而可予忽略。
方差分析的基本思想是把样本中存在的总变差(以“平方和”表示)分解成处理之间（或组间）的变差和处理内部（或组内）的变差，即

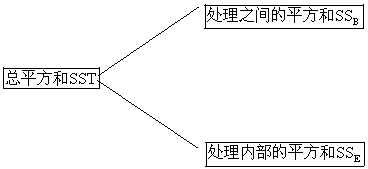
然后把它们的平方和变成方差（除以各自的自由度），进而把这两种方差作比，即

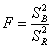
显然，这个统计值服从于F分布。
如果实验处理不发生作用，则SB2与SE2就可看成均来自同一总体的随机变差，即SB2与SB2相差不大，比值近似于1；如果实验处理发生了明显的作用，则SB2就不能看作是随机变差，而是看作来自含处理在内的更大总体的变差，这时SB2必大于SB2，比值就远大于1，即统计值F将落入F分布的右尾。因此，当计得F值落入F分布的右尾时，我们就否定处理之间没有差异的假设。
单因素的方差分析 对一种变量实施K种不同处理的结果，进行上述的方差分析，就称为单向方差分析。
当在K种实验处理之间有明显的差异时，我们还要区别造成这种差异是由于处理条件不同、还是由于某些处理的总体方差本来就较大呢？为此，对K种处理或K个样本进行方差分析时，必须假定这K个正态总体的方差相等或近似。有了这个假定，我们就可断定K种处理间的明显差异，主要是由于实施不同实验处理所致。
[例] 为鉴定4种不同数学教材的效果，分别在教师和学生水平相同的4所学校中各试行一种教材。经过一教学阶段后，从各校的试验班中随机抽取10个学生进行统测，结果如下：
教材Ⅰ:38 40 42 49 34 48 35 34 48 39教材Ⅱ:44 40 38 41 59 48 49 42 54 23教材Ⅲ:61 40 54 64 50 45 50 30 46 63教材Ⅳ:48 59 63 45 37 58 52 54 40 60问：这4种不同教材的教学效果是否有显著差异？
显然，这4种教材的平均数不同，说明存在处理或条件变差；其次同一种教材下的学生成绩也不同，说明存在随机变差。为了检验不同教材的效果，可以对每对平均数作显著性检验，但需作C42=6次的检验，这样做不但耗时费力，而且降低检验的可靠性。方差分析可以较好地解决这一问题。为此设H₀:u₁＝u₂＝u₃＝u₄。
第一步求各处理的平均数和标准差：₁＝40.7、S12=34.5、2=43.8、S22=96.8、3=50.3、S32=115.8、₄＝51.6、S42=78.5(总平均数r=46.6)。
第二步依下式求处理之间（或组间）的方差：

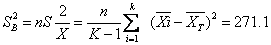
第三步依下式求处理之内（或组内）的方差：

第四步计统计值：

第五步作显著性检验。据f₁＝k-1=3,f₂＝k(n-1)=36及a=0.05，在F分布表中可查到F(_3,36)0.95＝2.872。因F>F(_3,36)₀.₉₅，故拒绝H₀，即认为不同教材的效果是明显不同的。
兹把上述单因素（教材）方差分析的一般形式概括如下(见表1与表2)。

容量相同的单因素方差分析表

表1 (H₀:u1=u2=…=uK)

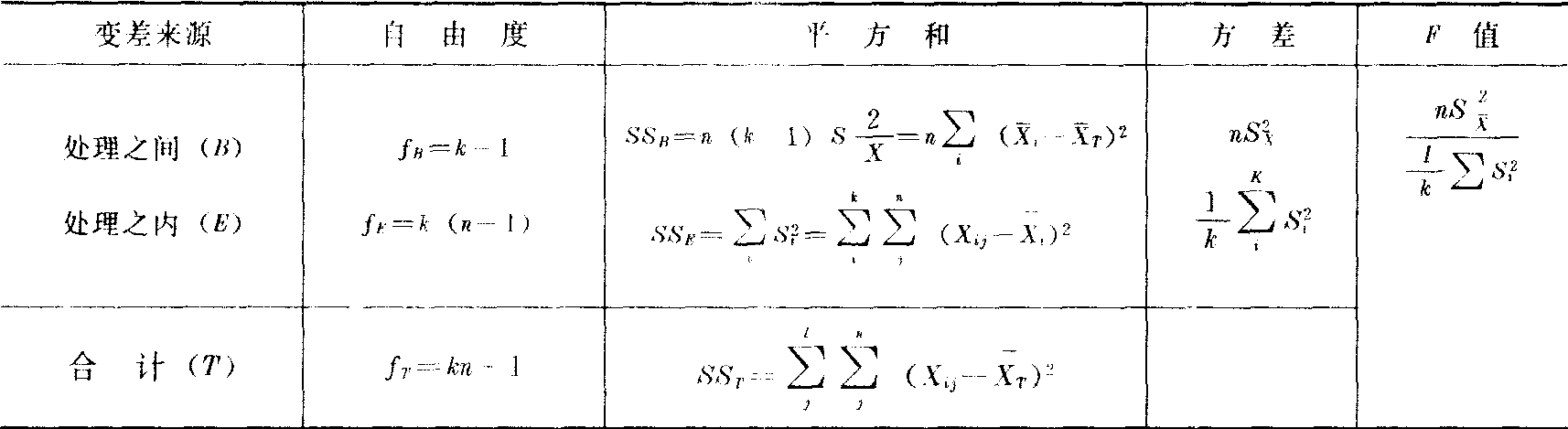
在上例中据表1的方差分析表为：

变差来源	自由度	平方和	方差	F值
教材之间 教材之内	3 36	813.3 2930.4	271.1 81.4	3.33*
合 计	39	3743.7

当容量不同时，则表1变为表2:

容量不同的单因素方差分析表

表2 (H₀:u₁＝u₂＝…=u_k)

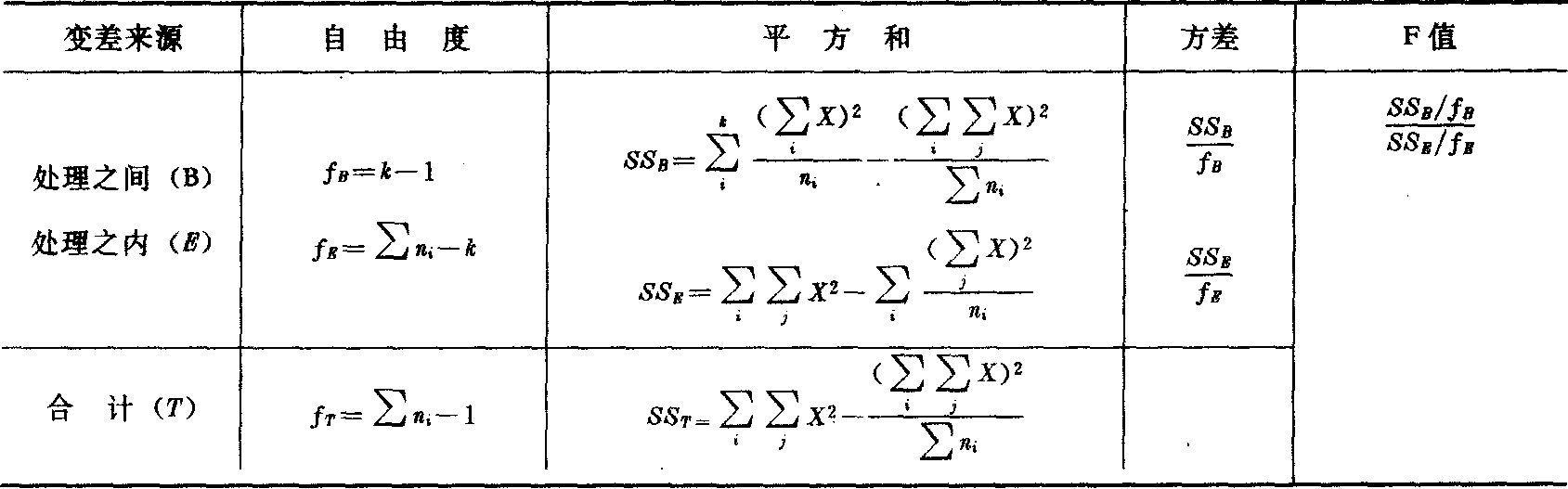
双因素的方差分析(见表3与表4)
表3 双因素方差分析的记数法

双因素方差分析表

表4=H₀:u₁＝u₂＝…=u_k,H′₀: u′₁＝u′₂＝…= μ′_k

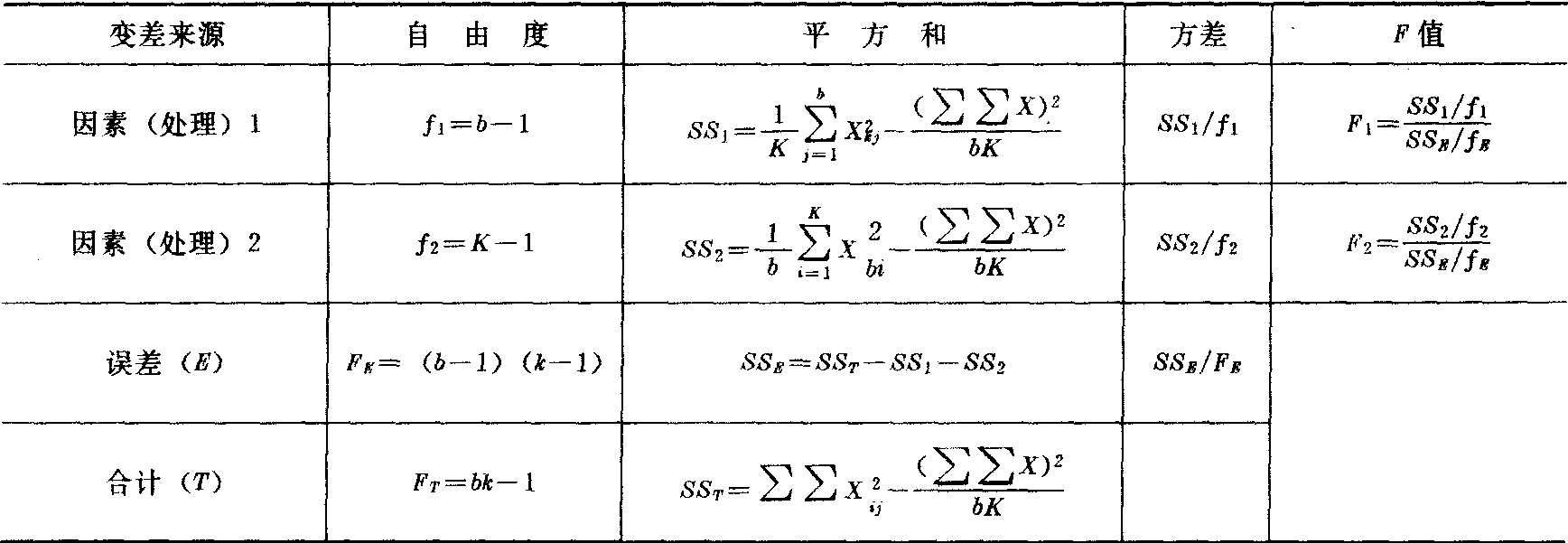
其他方差分析都可按表2和表4的基本思路来处理。此后不一一累述。

方差分析

一种常用的数理统计方法。通常利用分解子样与其均值之差的平方和来处理试验结果。分析某些因素对试验结果的影响。20世纪20年代英国统计学家首先应用于农业试验中。现已广泛应用于农业、工业、生物学、医学等方面。

方差分析variance analysis

亦称变异数分析或F检验，是数理统计中处理试验结果常用的一种方法。通过方差分析，可以检验各组均数间的差别是否显著。方差分析常作成方差分析表进行。作方差分析的资料必须满足资料分布的正态性、方差齐性、效应可加性三个条件。由于实验设计不同而有不同种类的方差分析模型。

方差分析Variance Analysis

亦称“变异数分析”，或称“F检验”。用于两个或两个以上样本均数差别的显著性检验。由于各种因素的影响，研究所得的数据呈现波动状。造成这种波动的原因可分成两类：
❶不可控的随机因素；
❷研究中施加的对结果形成影响的可控因素。

方差分析

根据方差分解的信息，用来估计和检验这些因素及水平的作用是否存在显著差异的方法。是对实验数据或其他统计数据进行统计分析和检验的一种有效方法。在一般的方差分析中，要把研究对象 （变量） 的方差分解为若干有意义的分量，例如根据若干不同影响因素及其不同水平来划分。

方差分析variance analysis

根据方差分解的信息，用来估计和检验这些因素及水平的作用是否存在显著差异的方法。是对实验数据或其他统计数据进行统计分析和检验的一种有效方法。在一般的方差分析中，要把研究对象（变量）的方差分解为若干有意义的分量，例如根据若干不同影响因素及其不同水平来划分。

方差分析

方差分析又称变异数分析(R. A. Fisher,1928)，其基本思想是把全部观察值之间的变异——总变异，按设计和需要分为二个或多个组成部分，再作分析。如分析单因素的完全随机设计的实验资料时，总变异可分为组间变异——表示各处理组均数间的变异，和组内变异——表示同一组内个体间的变异，通常称误差；分析配伍组设计的资料时，总变异可分为三部分： 处理组间变异、配伍组间变异及误差；分析2×2析因设计资料时，总变异可分为四部分：分属于两个因素的两个组间变异、两因素交互作用及误差。
单因素完全随机设计的方差分析中，组间变异或组内变异，均以离均差平方和(SS)除以相应的自由度所得均方(MS)表示。而组间均方与组内均方之比为F值。F值是方差分析中的统计量。

式中MS组间为组间变异的均方，表示样本均数间的变异。造成此变异可以有两种原因：第一，各组内个体间的变异； 第二，各组所接受的不同处理——试验因素的作用。其中第一种原因必然存在，第二种原因正是试验所要研究的问题。MS组内为组内变异的均方，纯由上述第一种原因造成，而与试验因素无关。因此，在上式中，若试验因素确有作用，将出现MS组间明显大于MS组内，因此F值也明显大于1；否则，MS组间与MS组内相近或相等，故F值近于或等于1。在方差分析中，以F值的大小检验各处理组的差别，经查F界值表得P值，即可按所取检验水准作出推断结论。F界值表中v₁为分子均方的自由度，v₂为分母均方的自由度。
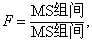
方差分析的用途：
❶两个或多个样本均数的比较；
❷分离各有关因素并分别估计其对变异的影响；
❸分析两因素或多因素的交互作用等。
应用方差分析的条件：
❶各个因素每一水平所得的样本都是随机样本；
❷各随机样本相互独立；
❸各个因素每一水平的重复试验数据都服从正态分布，且各个总体方差相等。

方差分析

见“F检验”条。

方差分析analysis of variance

在正态总体及方差齐性等基本假定下，通过F检验法作多个总体的均值是否相等的显著性检验的统计方法。即对试验结果数据进行分析，以检验变异因素影响是否显著的方法。为考察变异因素A,A的m个水平A₁，…，A_m，形成m个独立的正态总体X_j,X_j服从N(μ_j,σ_j²)(j=1，…，m)。在σ₁²＝…=σ_m²＝σ²的假定下，需检验H₀:μ₁＝μ₂＝…=μ_m。从各总体分别抽取容量为n_j(j=1,2，…，m)的样本，各样本数据为X_ij(i = 1，…，n_j;j = 1，…，m)。从总的变差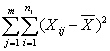出发，分解为因素A的不同水平引起的变差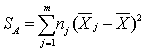与误差引起的变差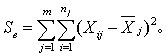在H₀成立下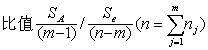，服从第一自由度m-1、第二自由度n-m的F分布。作F检验以判断因素A影响是否显著。
一个变异因素的情况为单因素方差分析，两个及两个以上因素的情况为多因素方差分析。考察多因素影响时要注意因素间的交互作用，要注意作实验设计的科学安排。方差分析的前提假定，如正态性、方差齐性等是否满足，可作检验；条件不满足时可作变量替换，或利用某些非参数方法作分析。
方差分析最初用于农业试验，以后广泛应用于农业、工业、生物学和医学等方面。

方差分析

利用试验结果的观察值与其平均数的离差平方和来分析某种因素变化对试验结果的观察值是否有显著影响的统计方法。经济现象是受许多因素影响的，通过方差分析，可以对各个因素的影响方式和程度作出判断从而选出最优方案。例如，分析小麦生产中采用不同种籽和不同肥料，对小麦单产有无显著影响； 工业生产中采用不同等级的原材料和不同工艺对产品质量有无显著影响。实际工作中，只就某一个因素进行试验的，称为单因素试验的方差分析；就多因素进行试验的，称为多因素试验的方差分析。

方差分析variance analysis

通过对因变量的分解、比较各部分变差的大小来检验各个自变量对因变量有无显著影响的统计分析方法，亦称“离差分析”，“变异数分析”。参数检验法之一。方差分析是对多个正态分布总体间的平均数作统计假设检验的一种常用方法。它根据实验中独立观察值与平均数之差的平方和来分析实验中的某一因素或多种因素对实验结果的影响程度，从而确定出对实验结果起主要影响作用的因素所在。就单因素的方差分析而言，它所讨论的问题可归结为：设有K个正态总体X₁,X₂，…XK，分别有总体平均数U₁,U₂,U₃, …UK和总体标准差σ1、σ2，…σK的条件下， 问这K个总体平均数是否相等。可建立如下的统计假设：

H0: U₁＝U₂＝U3=…=UK

检验假设的具体步骤是：(1)在一定的α, β与允许误差情况下确定样本容量n，抽取样本并获得实验数据。(2)计算统计量，将反应量的总平方和分解为归因于各实验变量、交互作用和实验误差几个变异源的平方和，其次将各平方和除以相应的自由度，得出各变异源的方差，称作均方，然后按一定要求逐对选取两个相应的均方相比，构成各F统计量。(3)根据α确定统计量F的接受域，即先定F的临界值Fα的数值。(4)根据F与Fα值的比较结果作出统计推断结论。多因素方差分析的基本程序和方法与单因素方差分析基本相同。

方差分析analysis of variance

简称ANOVA。亦称“变异数分析”。用于两个及两个以上样本均数差异的显著性检验。英国统计学家费希尔(Ronald A. Fisher, 1890—1962)提出。由于各种因素影响，研究所得数据相互间呈现一定差异，因素主要包括： (1) 不可控的随机因素；(2) 研究中施加的对结果产生影响的控制因素。方差分析通过分析描述数据变化（即差异）的方差，研究不同因素影响，找出对观测变量有显著影响的因素、各因素间交互效应以及显著影响因素的最佳水平等。心理学研究中，方差分析主要用于实验数据的处理和分析。方差分析的基本条件包括： (1) 方差齐性；(2) 变异可分离；(3) 数据服从正态分布。根据方差分析过程中自变量个数，可分为单因素分析、多因素方差分析。

方差分析

亦称“变异数分析”。通过分析实验数据中不同来源的变异对总变异的贡献大小，从而确定实验中的自变量是否对因变量产生重要影响的统计分析方法。由英国统计学家费希尔(R.A.Fisher)在1926年左右提出。分析的方法主要通过F检验进行。