数学规划mathematical programming

在一定约束条件下解目标最优化问题的数学方法。又称规划论、数学规划论。是运筹学（见运筹学模型）重要分支之一。它应用于最优化设计，资源配置与管理等方面。构成一个数学规划问题的基本要素是：❶决策变量，反映系统内部要作出决策的具体对象；
❷约束条件，是决策变量所受到的限制，表示为决策变量的函数方程和不等式；
❸目标，决策人所选择的变量系统效益的指标，表示为决策变量的函数，称为目标函数。数学规划包括线性规划、整数规划、多目标规划、动态规划、非线性规划、组合规划、随机规划、模糊规划、参数规划、几何规划等。
线性规划 目标函数和约束方程都是线性的数学规划。1939年苏联数学家坎托罗维奇(Л.В.Канторович)发表的《生产组织与计划中的数学方法》一书，是有关线性规划的最早文献。1947年美国丹齐克(G.B.Dantzig)提出线性规划问题的一般形式和单纯形法后，使线性规划得到了较多的应用，电子计算机技术的进展，对线性规划的发展起了很大的推动作用。它是运筹学中应用最广的一个分支。线性规划还可结合投入产出法，网络分析法，对策论等方法建立相应的最优化模型。
线性规划的标准形式：

目标函数：

满足约束：

也可用矩阵形式表示：

式中

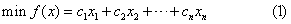
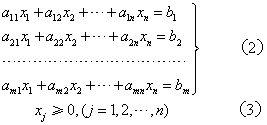
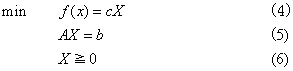
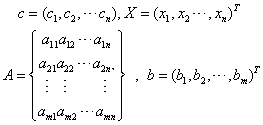
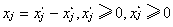m为约束条件方程数，n为变量数，一般mj(j=1,2，…，n)为决策变量，a_ij、b_i、c_j是常数，统称为模型参数，决策变量为负值时对实际系统没有意义，故有非负约束x_j≥0，实际构造的线性规划数学模型与标准形式不一致时，需作必要的数学变换。当问题中包含不等式约束a_i1x₁+a_i2x₂+…+a_inx_n≤b_i或a_i1x₁+a_i2x₂+…a_inx_n≧b_i时，可加（或减）一个非负的松弛变量x_n+i，使之化为等式a_i1x₁+a_i2x₂+…+a_inx_n±x_n+i=b_i。若问题是求目标函数f(x)的最大值，则可等价地化为求-f(x)的最小值。若变量x_j无非负要求，则可令，再代入各式。例，某地计划生产两种农产品x₁和x₂，生产100千克产品x₁需消耗农用物资A 3千克，消耗物资B 1千克，而生产100千克产品x₂需要消耗农用物资A 2千克，B2千克，农用物资A和B的可供应量分别是12千克和8千克，两种农产品可获得的销售利润分别为x₁＝0.3元/千克，x₂＝0.4元/千克。求如何安排产品x₁和x₂的产量，以获得最大销售利润。上述问题是要确定x₁和x₂的值，满足约束条件：3x₁+2x₂≤12,x₁+2x₂≤8,x₁≥0,x₂≥0，使目标函数f(x)=30x₁+40x₂取最大值。通过引入松弛变量x₃,x₄，可化为标准形式：max f(x)=30x₁+40x₂
满足约束：3x₁+2x₂+x₃＝12
x₁+2x₂+x₄＝8
x^j≥0,(j=1,2,3,4)该例可用图解法求解(图1)，图1中各约束方程所围成的阴影区域ABCO上的每个点（包括边界上的点）都是满足约束条件的解，为可行解，该区域为可行域。A、B、C、D为顶点（可行域有时也可能无界）。目标函数f(x)=30x₁+40x₂，在坐标平面上是随f (x)取不同定值时的一族平行的等值线。位于同一直线上的点，具有相同的目标函数值。如图1中虚线所示。其中通过可行域顶点B的目标函数值最大，所以B点对应最优解，即x₁＝2, x₂＝3（百千克）f(x)=180（元）。图解法不适于求解高维问题。丹齐克提出的单纯形法，则是解高维线性规划问题的一种基本方法。它是基于凸集理论，即线性规划问题在几何学上，相当于满足线性约束集所构成的凸多面体（可行域），每一个顶点对应于线性规划问题的一个可行解，且满足非负约束，故又称为基本可行解。可以证明，线性规划若存在最优解，必在可行域顶点上达到，如图1中的B点所示。这是线性规划解的一个基本性质。因此，通过顶点的每一次迭代逐次改善目标函数值f(x)，当达到某一顶点，不再能改进目标函数值时就得到最优解。单纯形法可以用单纯形表来实现。

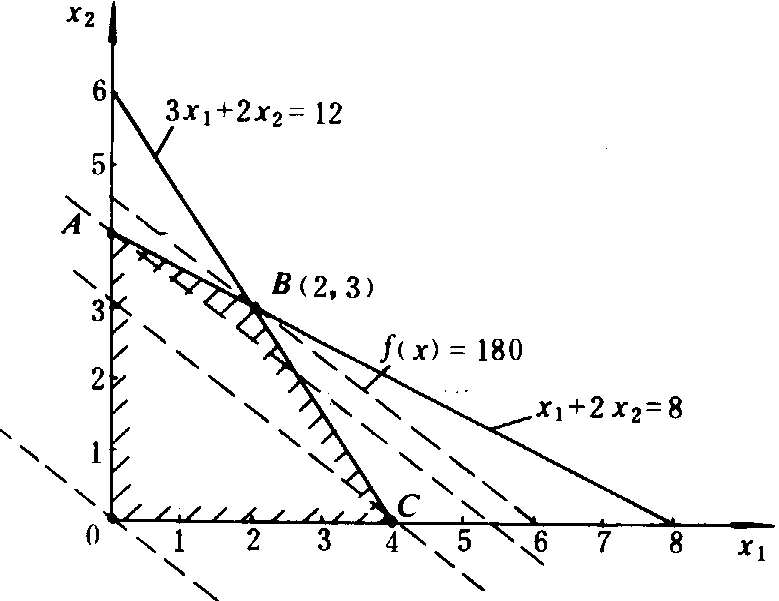
图1 两种产品产量的可行域和最优解

对偶问题 任一线性规划问题（称为原问题），都存在另一个与它互为对偶的线性规划问题，称为对偶问题。设线性规划的原问题为：目标函数：

maxf(x)=cx (7)

满足约束：

AX≤b (8)

X≥0 (9)

其对偶问题为：目标函数：

ming(Y)=Yb (10)

满足约束：

YA≥c (11)

Y≥0 (12)

式中 Y为1×m列向量。若问题有最优解，两者的目标函数值相等，即maxf (x)=min g(Y)。若原问题有可行解，但无最优解，则对偶问题无可行解。有时把原问题变换成对偶问题更便于求解。y_i称为对偶变量。当得到实际问题的最优解时，Y_i是第i种资源在实现最大利润时的一种价格估计，也称为资源b_i的影子价格或机会成本。当y_i＝0时，表明第i种资源有剩余，原问题中对应的第i个约束方程的松弛变量大于零。当y_i≠0时，表明第i种资源已充分利用，原问题中对应的第i个约束方程的松弛变量等于零。在保持原问题最优解的情况下，增加资源投入量△b_i，引起目标函数值增量为△f(x)=△b_ixy_i,y_i＝△f(x)/△b_i，所以，对偶变量y_i相当于资源b_i的边际生产力。
敏感性分析 （又称优化后分析）实际问题中，参数a_ij、b_i和c_j并非有唯一确定值。当其变动超出允许范围时将使问题的最优解发生变化，甚至不再是最优解。在保持问题最优解的情况下，分析参数a_ij、b_i和c_j允许变动的范围，称为敏感性分析。
运输问题 以最小的总运费将物资由m个供应地（称发点）运至n个需求地（称收点）的调运规划问题。这是一类特殊的线性规划问题。其数学形式为：目标函数：

满足约束：

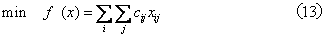
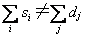式中 x_ij是第i个发点运到第j个收点的运输量。c_ij是第i个发点到第j个收点的单位运输量的费用。dj是第j个收点的需求量。s_i是第i个发点的供应量。对于的供需不平衡运输问题，可设置松弛变量，并引入相应的虚发点或虚收点。由于运输问题的特殊结构，其基本可行解仅有(m+n-1)个，且必存在一最优解。求解运输问题的简便方法有图上作业法和表上作业法。
中国在1958年运用表上作业法规划物资调运。1980年以后，线性规划已在中国农业区域经济发展规划、农业生产的劳（力）畜（力）机械优化配备、饲料配方、农业投资分配等方面应用。1984年建立的中国种植业发展结构线性规划模型含8702个变量和3287个约束方程。国际上如1975年美国农业和农村发展中心的线性规划模型(CARD)，其中最大的一个模型含75 000个变量和10 000个约束方程。
整数规划 要求全部或部分变量取整数值的数学规划。实际问题中的许多变量，如机器台数、人数等必须是整数，而线性规划的解不一定是整数，若简单地圆整为整数，其解不能保证是整数可行解或最优整数解。整数规划可分为纯整数规划和混合整数规划。前者要求全部变量是非负整数；后者仅要求部分变量是非负整数。当变量取值限制为0或1时，称为0—1规划。
线性整数规划 目标函数和约束方程是线性的整数规划。一般是在解线性规划问题基础上，采用分解算法和割平面法求得问题的最优整数解。给定整数规划问题A:minf(x)，满足约束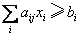和x_j≥0，且是整数，i=1,2，…，m,j=1,2，…，n。分解算法需要首先放弃问题A的某些约束条件（通常是整数约束），以构成它的一个松弛问题B求解。这类分解算法包括分枝定界法和隐枚举法等。
分枝定界法 以下面的整数规划问题(A)为例。求：

maxf(x) =3x₁+x₂ (1)

满足条件：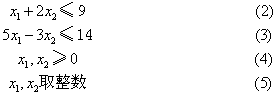

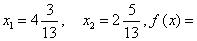
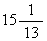不考虑整数约束条件(5)，构成问题(A)的松弛问题(B)求解，得最优解，即图2中的A点，考察其中任意一个非整数变量，例如选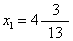，可以认为x₁的最优整数解值是x₁≤4或x₂≥5。因为在4与5之间不满足整数条件(5)，于是可将问题(B)分解为两枝：新增约束条件x₁≤4的问题(B₁)；和新增约束条件x₁≥5的问题(B₂)。问题(B₁)的最优解为x₁＝4,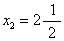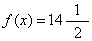，即图2中的A₁点。问题(B₂)无可行域。因仍未得整数解，在问题(B₁)中，考察仍为非整数的变量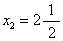，进一步分解得：新增约束条件为x₂≤2的问题(B₃)和新增约束条件为x₂≥3的问题(B₄)。问题(B₃)的最优解为x₁＝4,x₂＝2,f(x)=14，即图2中的A₂点；问题(B₄)无可行域。于是得到问题A的最优整数解为x₁＝4,x₂＝2,f(x)=14(图2中的A₂点)。全部求解过程如图3所示。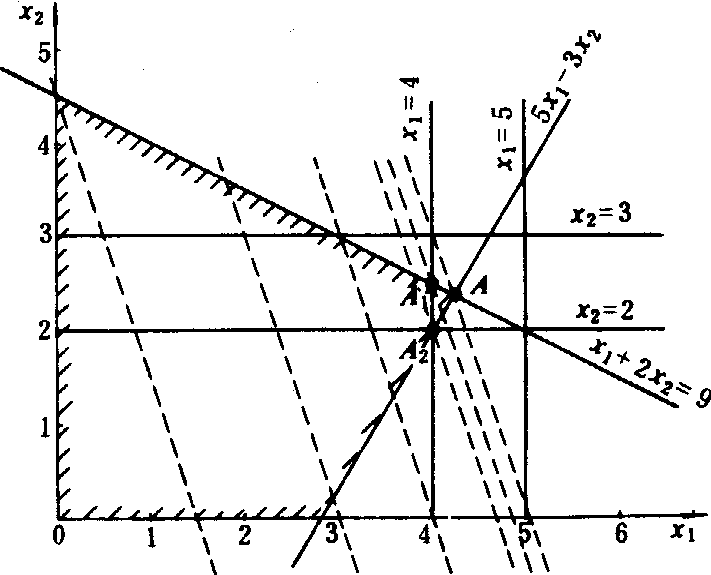

图2 分枝定界法的求解

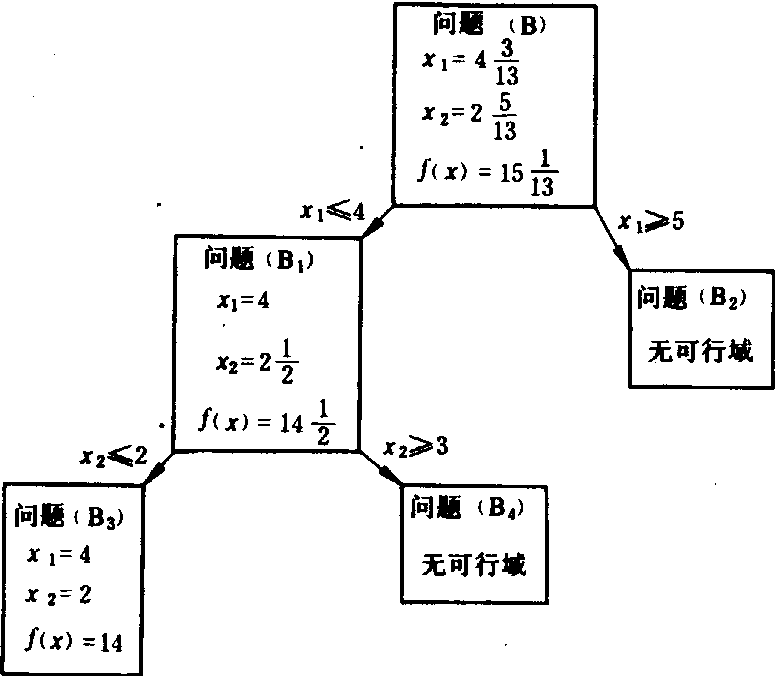
图3 分枝定界法求解过程

割平面法 仍以上例说明。首先求松弛问题(B)的最优解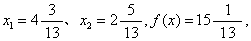即图4中的D点。其次在式(2)和式(3)中分别引入松弛变量x₃,x₄，得：

x₁+2x₂+x₃＝9 (6)

5x₁-3x₂+x₄＝14 (7)

然后把非整数的基变量x₁和x₂用非基变量x₃、x₄来表示，得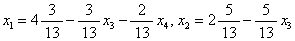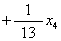。因为x₁、x₂、x₃、x₄都必须取整数，故可得同余方程：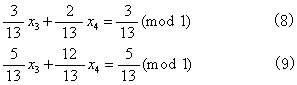

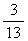利用同余方程(8)中x₃和x₄的系数可导出一个新的约束条件，例如，用乘式(2)两边，用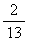乘式(3)两边，然后把这两式相加，得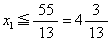。由于x₁必须为整数，因此得到一个新的约束条件x₁≦4。x₁＝4就是整数规划的一个割平面。问题B增加这一约束条件后的最优解为图4的D₁点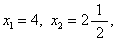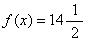，。再用同余方程(9)中x₃和x₄的系数分别乘式(2)与式(3)两边后两式相加，可得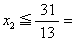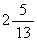。由于x₂必须为整数，得到又一个新约束条件x₂≤2,x₂＝2是又一个割平面。再增加此约束条件后的最优解为图4的D₂点，x₁＝4,x₂＝2,f(x)=14。它就是整数规划问题A的最优解。
多目标规划 研究具有多于一个目标函数问题的数学规划。也称多目标最优化。是数学规划的一个分支。1896年意大利经济学家帕雷托(V.Pareto)从经济学角度提出多目标最优化问题，并用权系数法解决了某些实际问题。1951年库普曼斯(T.C.Koopmans)最先引入了解的有效性概念。用来描述多目标规划最优解的性质，从而给出了多目标最优化的确切含义。农业系统实际问题大多有多目标要求，因而，多目标规划的研究与应用有重要意义。

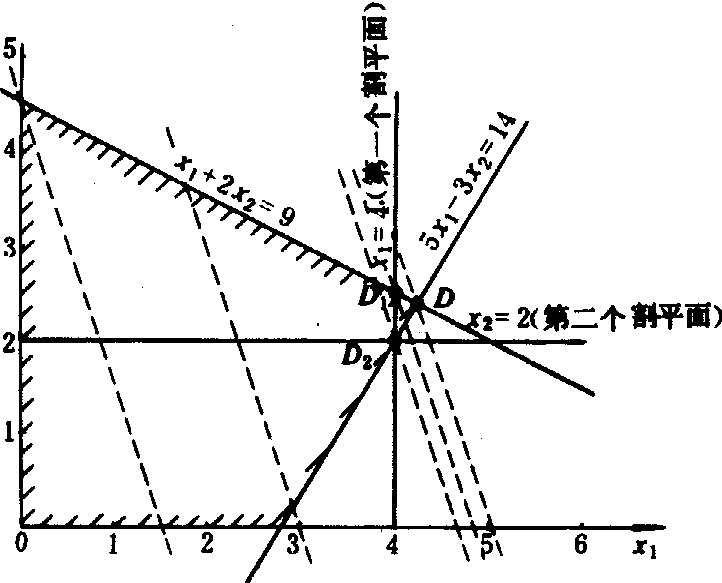
图4 割平面法的求解

分类 多目标极小化问题通常记为(VMP):V-f (x)，此式表示目标向量f (x)=【f₁(x),f₂(x)，…，fp(x)】^T，在区域x(XRⁿ)上，多个目标被同等级地极小化，V-min表示这是一个多目标规划问题。若构成的问题的目标向量f(x)和约束是x的线性函数，称(VMP)为多目标线性规划问题；若目标向量f(x)和约束不都是x的线性函数，称(VMP)为多目标非线性规划问题。
解的有效性 多目标规划问题一般不存在绝对最优解，即使得各目标同时达到最优，这就需要引入有效解和弱有效解等概念。如果存在一个可行解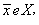对于其他的可行解x，使得f(x)>f()(在向量的各目标分量间都存在“>”关系)，则称为(VMP)问题的有效解或帕雷托最优解，也叫非劣解。如果存在一个可行解∈X，对于其他的可行解x，使得f (x)≥f()，且至少有一个目标分量之间是“=”关系，则称是(VMP)问题的弱有效解。多目标规划问题常存在多个有效解，由于各个有效解之间的不可公度性，即各个目标在本质上不能用同一个标准来度量。因此，有效解的选择与决策人的偏好函数有关，这也是多目标规划研究中的一个重要领域。
多目标规划的算法 一般情况下是把多目标规划问题转化为单目标规划问题求解，如约束法、线性加权和法、分层求解法和参考点法。
约束法 设目标向量f(x)有p个目标分量f(x)=〔f₁x,f₂(x)，…，f_p(x)〕^T，按照各个目标的相对重要性，选择其中最重要的一个目标设为主目标记为f_k(x)，其余目标则按设定的期望值b0i转化为(VMP)问题的约束条件f_i(x)=bOi，从而构成一个单目标规划问题求解。多目标线性规划问题可表示为：目标函数：

minf_k(x) (1)

满足约束：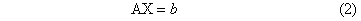

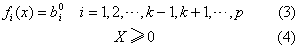
如果存在最优解，则是该(VMP)问题的有效解。
线性加权和法 把多目标规划问题的各个目标，赋以不同的线性权系数ω_i,并满足ω_i＝1，得到一个目标函数为F(x)=ω^Tf(x)的单目标规划问题。当ω_i>0,i=1,2，…，p，则其最优解是多目标规划问题的有效解，如果权系数分量中至少有一个ω_i＝0，则即为弱有效解。选取不同的权系数向量，将得到不同的有效解或弱有效解。权系数依据实际问题的背景和决策人的偏好而定。这种方法需要对多目标进行量纲和目标优化方向（极大或极小）的一致性处理。
分层求解法 把目标向量f(x)=〔f₁ (x),f₂(x)，…f_p(x)〕^T中的目标，按其重要程度进行排序，设f₁(x)>f₂(x)>…>f_p(x)，然后依优先次序逐级转化为单目标规划求极值。例如，先求解以f₁(x)为目标的单目标规划问题，得到最优解₁和目标函数值f₁^*。再求以f₂(x)为目标的单目标规划问题：

得到相应的最优解₂和目标函数值f₂^*。依次按下列格式求解，直至求得以f_p(x)为目标的单目标规划问题的最优解。

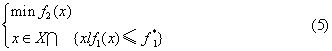
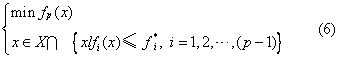
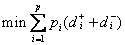所求得的最优解_p，即为(VMP)问题的有效解。也可以给目标f_i(x)增设偏差变量d⁺_i和d^-_i分别表示目标的超过和不足，用上述方法求目标向量的极小化，可转化成求目标的偏差变量极小化：,p_i为各目标按其相对重要程度的优先级别，设p₁≻p₂>…>p_p，则求第p个目标是偏差变量极小化即为：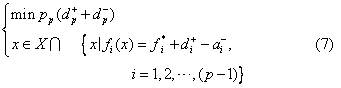

f_i^*为目标希望值。
理想点法 分别按各个分目标f_i(x),i=1,2，…，p，求极小值f^*_i得到目标向量f^*＝(f^*1,f^*₂，…f^*_p)^T。由于向量f^*的各个分量对于相应的分目标而言是最理想的值，故称f^*为(VMP)问题的理想点。但这种状态一般是不可能的。理想点法的基本思想就是使得所求的目标向量f(x)与(VMP)问题理想点f^*的偏差极小。如果把这种偏差视为距离，可以定义一个标量化罚函数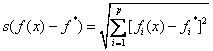因此(VMP)问题就成为求偏差函数s的极小化问题，所得到的最优解就是问题(VMP)的有效解。求理想点太理论化，因此有人提出用希望值或参考点来代替理想点。1979年威尔兹贝克(A.P.Wierzbicki)基于参考点理论提出了参考点法，广泛应用于交互式多目标决策分析系统。
动态规划 研究决策过程最优化问题的数学规划。由于决策过程常常可以离散化为多个决策阶段，故又称多阶段决策。1951年美国数学家贝尔曼(R.Bellman)提出最优性原理，1957年他发表《动态规划》专著。动态规划可应用于管理和最优控制，如农业工程项目投资决策、农业规划、水资源调度、生产库存与设备更新、农业资源分配、农业运输等。
基本概念 以农产品运输的最短路线问题为例(图5)。农产品由A点运到D点可分为三个阶段，有多条备选路线，求其中运输距离最短的路线。第一阶段由A出发，有两个备选点：B₁和B₂。若选B₁，则B₁就是第一阶段的结果，也就是第二阶段的出发点。第二阶段从B₁出发有三个备选点：C₁、C₂和C₃。若选C₁，第三阶段就从C₁开始通到终点D。此时构成一条路线AB₁C₁D。总距离为AB₁+B₁C₁+C₁D=5+4+3=12。有五个基本概念：❶阶段，把一个系统决策过程按时间或空间划分成相关联的子过程。若阶段数有限，为离散决策过程。若阶段数无限，为连续决策过程。在图5中，阶段是按顺序编号的，也可逆序编号。
❷状态，用以描述系统在各个阶段上的时空位置，如各个阶段的始点就代表该阶段的状态。描述状态的变量称状态变量，常用K表示第k阶段的状态变量，一般每个阶段都有若干个可能的状态，如第三阶段的状态集合为{C₁,C₂,C₃}。若状态是确定的，就称为确定性动态规划，若系统状态是随机的就称随机性动态规划。状态要满足无后效性，即给定某一时刻的状态（称为当前状态），此时刻以前的过程只能通过当前状态去影响以后过程的发展，而不能直接影响未来的发展。
❸决策，当给定某个阶段的状态x，对下一阶段的状态所作出的选择。描述决策的变量称为决策变量，记为u_k(x_k)，它是一给定时刻状态x_k的函数，可以是一组数或一向量。实际问题中决策变量的取值限制在某一范围，称为允许决策集合，记为D(x_k)，则有u_k(x_k)∈D(x_k)。例如图5中从B₁点出发的允许决策集合D(B₁)={C₁,C₂,C₃}。相应的路程为{4,6,7}，若选取的点为C₁，则u₂(B₁) =C₁。
❹策略，从始点到终点的各阶段决策的序列称为一个策略。实际问题中都存在若干备选策略。全体备选策略称为允许策略集合，记为{u₁(x₁),u₂(x₂)，…，u_n(x_n)}。各阶段的决策变量u_k(x_k),(k=1,2，…，n)取值不同就得到不同策略，其中使全过程整体效益最好的决策称为最优策略。最优策略不一定是唯一的。如上例中AB₁C₁D和AB₂C₂D两条路线的距离都是12，均为最短，所以有两个最优策略： {A,B₁,C₁,D}和{A,B₂,C₂,D}。
❺指标函数，用以衡量决策过程优劣的一种指标，是x和u的函数，记为V(x,u)。在离散确定性问题中，通常是各阶段指标函数V(x_k,u_k)的加或乘。上例中求运输距离最短的指标函数就是各阶段指标函数的加：

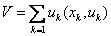
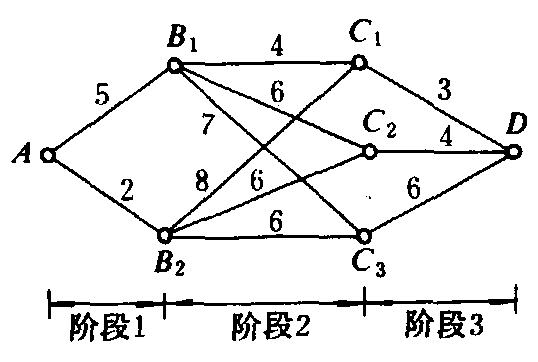
图5 多阶段决策

贝尔曼的最优性原理 最优策略具有这样的性质：不论初始状态与初始决策如何，对于先前的决策所造成的状态而言，下余的那些决策必构成一最优策略。它是动态规划问题解法的基本依据，由此导出动态规划基本方程。
动态规划基本方程 离散确定性决策过程的动态规划基本方程为：

式中 k是阶段号。f_k(x_k)是第k阶段开始的子过程的指标函数的最优值。*号代表加法或乘法运算关系。opt代表max或min。这是满足边界条件方程式(2)的递推决策的函数方程，它由最终阶段n开始，逆向依次进行决策。决策过程也可由始点向终点顺序递推。此时的动态规划基本方程为：

求解动态规划问题时要建立状态转移方程x_k+1＝T(x_k, u_k)或x_k-1＝T(x_k,u_k-1)，它是给定时刻的状态与决策的函数，上例中，第三阶段的状态x₃由从B₁出发的第二阶段的状态x₂＝B₁和第二阶段的决策u₂(B₁)来确定，x₃＝T〔B₁,u₂(B₁)〕=C₁。由于每个动态规划问题有各自的状态转移方程，所以，动态规划没有数学模型的标准形式和通用的算法。
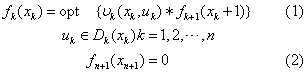
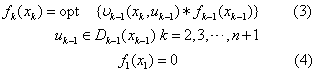
动态规划解法的主要特点是把n个变量的极值问题分解为n个单变量的极值问题，而且避免了穷举。
非线性规划 目标函数或约束条件中至少有一个是非线性函数的数学规划。
数学模型的一般形式 非线性规划的数学模型常写成以下形式：目标函数：

minf(x) (1)

满足约束：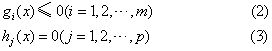

式中 x=(x₁,x₂，…，x_n)^T是n的维欧氏空间Eⁿ中的向量；f(x)为目标函数；g_i(x)≤0和h_j(x)=0为约束条件。求f(x)极小可等价为求-f(x)极大，故式(1)不失其一般性。
计算方法 目前尚无通用算法。一般都用迭代算法，即逐渐逼近所求的解。通常按约束条件分为无约束极值问题和约束极值问题两大类。
无约束极值问题 在非线性规划中占有重要地位，除了本身的意义与应用外，它也是许多计算有约束极值问题的基础。
❶直接法。迭代中仅计算和比较函数值来逐步逼近最优解的方法。计算简便，但收敛较慢，只在变量较少时才适用。常用的有鲍威尔法，单纯形调优法和模式搜索法。
❷间接法。特点是在迭代中需要计算目标函数的一阶或高阶导数。常用的是以梯度法为基础的最速下降法、牛顿法和变尺度法。设有迭代公式：

式中t_k为步长；H_k为n×n对称矩阵；▽f(X_k)为目标函数梯度。令H_k为单位阵，即可得最速下降法；令H_k＝〔H(X_k)〕^-1，其中H(X_k)为海赛矩阵得到牛顿法。最速下降法的收敛速度慢；牛顿法虽然收敛速度较快，但求逆阵〔H(X_k)〕^-1较困难。而变尺度法则在迭代过程中逐次构成一个矩阵H_k，使H_k逼近〔H(X_k)〕^-1，利用式(4)进行迭代时，既可保证二次收敛性质，又不需要计算逆阵〔H(X_k)〕^-1。于是，变尺度法(又称DFP法)成为一种最常用的算法。
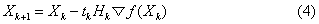
约束极值问题 按约束条件的不同而有不同的解法。仅有等式约束时，可化为无约束问题求解；兼有等式约束和不等式约束时，可将不等式约束化为等式约束，再进而化为无约束问题求解；兼有线性约束和非线性约束时，可将问题化为线性问题，用线性逼近的方法求近似解。常用的有可行方向法，梯度投影法，拉格朗日乘子法，罚函数法，近似规划法等。
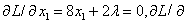
拉格朗日乘子法应用拉格朗日乘子λ把目标函数与约束等式联系起来。设有等式约束h(X)=0，求minf(X)。构造一个拉格朗日函数L(X,λ)=f(X)+λh(X)，于是把原问题变为求函数L(X,λ)的无约束极值问题，其驻点条件为： ∂L/∂x_i＝0,∂L/∂λ=0。如求解minf(X)=4x₁²+5x₂²,h(X)=2x₁+3x₂-6=0,L(X,λ)=4x₁²+5x₂²+λ (2x₁+3x₂-6)。驻点条件为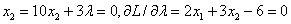：。因此解出： x₁^*＝15/14,x₃^*＝9/7,f(_x^*)=90/7。
罚函数法是根据约束的特点构造某种罚函数，然后把它加到目标函数上去，使有约束极值问题转化为无约束极值问题来求解。这种惩罚策略使违反约束的那些迭代点具有很大的目标函数值。于是使无约束问题的极值点或者无限地向可行集靠近；或者一直保持在可行集内移动，直到收敛于原来约束问题的极值点。
解的条件 为判断一个算法所产生的点是否为所给问题的解，需要知道解的必要和充分条件。库恩一塔克条件指出，局部极值点的必要条件是目标函数负梯度-▽f(X)可以表示为起作用诸约束方程的梯度的线性组合。在几何上这种条件表示为： 起作用约束方程的梯度向量构成一个锥体，目标函数的负梯度方向包含在此锥体内。一般地，这种条件并非是解的充分条件，但在约束条件函数都是凸的，而目标函数是凹的情况下都是充分的。

数学规划

即“规划论”。

数学规划

亦称“最优化理论”。研究目标函数在一定约束条件之下的极值问题的数学方法。数学规划包括线性规划和非线性规划、动态规划等。在军事上，可以应用线性规划解决兵器分配、部队中各种战斗兵器的配合问题、弹药及军需物资的运输，有限的资材在各机构之间的合理分配问题等。