支出函数expenditure function

在消费者理论中，如果消费者有表示其偏好关系≥的效用函数u(·)，则对于一个指定的效用水平u和价格p=(p₁，…p_e)，支出函数是为了得到效用水平不低于U所必须的最小支出，即支出函数v (p,u)定义为：

e (p,u) =min{px|u (x) ≥u}

对指定的收入水平W和价格p=(p₁，…p_e)，间接效用函数是消费者可能达到的最大效用水平，即间接效用函数V (p,w)定义为：

v (p,w) =max {u (x) |px≤w}

如果偏好关系遵从局部不满足性假设，则支出函数和间接效用函数互为反函数。例如设效用函数u (x₁,x₂₎ =x₁^ax₂^1-a，则对应的支出函数e(p₁,p₂,u) =kp₁^ap₂^1-au，其中k为与a有关的常数，用w代替e (p₁,p₂,u)，用v (p₁,p₂,w)代替u，则容易从支出函数求出对应的间接效用函数

v (p₁,p₂,w) =w/kp₁^ap₂^1-a

。

支出函数Expenditure Function

表示支出的最小值与商品价格和消费者效用之间的关系。由根据支出最小化一阶条件中所求出的各商品的希克斯需求函数代入预算函数导出。设预算函数为：

希克斯需求函数为：

支出函数定义为：

支出函数的实质是在给定价格的条件下，如何以最小的支出实现一个固定的效用水平。希克斯需求函数与支出函数的关系由霍特林(Hotelling)定理给出，即：

支出函数有以下性质：
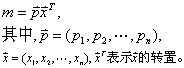
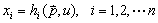
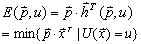
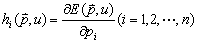
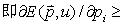(1)对是非递减的，0;
(2)对是一阶齐次函数，即E(,u)=tE(,u),t是任意大于零的常数；
(3)E(,u)是关于的凹函数，即对于任意¹, ²，有

(4)当>0时，E(,u)为连续函数。支出函数与间接效用函数的关系是：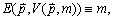
式中，V(,m)是间接效用函数。
〖参〗希克斯需求函数
　预算约束
　间接效用函数

支出函数expenditure function

在消费者理论中，如果消费者有表示其偏好关系≳的效用函数u(·)，则对于一个指定的效用水平u和价格p=(p₁，…，p_n)，支出函数是为了得到效用水平不低于u所必须的最小支出，即支出函数e(p,u)定义为：

e(p,u)=min{p·x|u(x)≧u}

对指定的收入水平w和价格p=(p₁，…，p_n)，间接效用函数是消费者可能达到的最大效用水平，即间接效用函数v(p,w)定义为：

v(p,w)=max{u(x)|p·x≦w}

如果偏好关系遵从局部不满足性假设(参见“偏好关系”)，则支出函数和间接效用函数互为反函数。例如设效用函数u(x₁,x₂)=x₁^αx₂^1-α，则对应的支出函数e(p₁,p₂,u)=K p₁^αp₂^1-αu，其中K为与α有关的常数。用w代替e(p₁,p₂,u)，用v(p₁,p₂,w)代替u，则容易从支出函数求出对应的间接效用函数v(p₁,p₂,w)=w/Kp₁^αp₂^1-α。