指数zhǐ shù

❶ 表示一个数自乘若干次的数字。1873年《代数术》卷一：“惟有时并写多字，殊觉不便，故用省字之法，但书其一而记其字数于本元之右角上，此数谓之指数，亦谓之方指数。”1896年《代数备旨》第一章：“凡一元字，或数元字彼此乘除，不论有系数及指数否，即为一项。”1931年《英汉对照百科名汇》：“Exponent，指数。”
❷ 某一经济现象在某时期内的数值和同一现象在另一个作为比较标准的时期内的数值的比数。1920年朱执信《米本位说之批评》：“假如照物价指数来算，米的价增到百分之一的时候，兑出的米从来一石的，现在就只兑九斗九升。”1924年王怡柯译《货币学》第十二章：“指数，index number。”1931年《英汉对照百科名汇》：“Index number，指数（经）。”1938年徐特立《目前政治形势与今后抗战的任务》：“物价指数之增长： 芦沟桥事变后半月增涨百分之五，九月中比八月又增涨百分之二。”

指数zhǐ shùндекс

指责缺点

抵瑕
指责别人的过失：谤
　从旁指责过失：诽
　议论是非，指责过失：非谤
列举过失加以指责：数(数叼；数落；～罪；面～其罪)　索落　排揎
　指责数落：指数
　责骂数落：诟数
寻究其失而指责：讨谪
直言指责过失：斥言
急切指责别人的过失：绞讦

指数

反映那些不能直接相加、不能直接对比的多因素组成的同类现象的综合变动的相对数。主要作用是测定同类现象变动的方向和程度，分析某种现象的变动受各种因素变动影响的程度等。利用指数来分析所研究的现象的方法称为指数分析法或指数法。按所反映现象的性质，可分为数量指标指数和质量指标指数；按计算方式可分为综合指数和平均数指数；按对比时所用的基期可分为定基指数和环比指数。

指数index

表明社会经济现象数量对比关系的相对数。广义的指数泛指一切比较相对数。狭义的指数专指某种不能直接同度量、指标值经加入同度量因素后方能进行汇总对比的特殊的相对数。通过指数的计算，既可以对多种事物的综合变动进行对比分析，也可以对复杂现象的变动进行因素分析。指数按反映现象范围的不同，可分为个体指数和总指数；按反映现象性质的不同，可分为数量指标指数和质量指标指数；按采用基期的不同，可分为定基指数和环比指数等。

指数

统计中反映各个时期某一社会经济现象变动情况的指标。某一社会经济现象的报告期数值对基期数值之比。分为个体指数和总指数。前者反映个别社会经济现象的变动，如说明个别产品的产量或成本变动指数。后者综合反映全部社会经济现象的变动，如说明多种商品价格或销售量、销售额等的总动态指数。

---

指数

见“幂”。

指数指數zhǐ shù

屈指计数。王世贞《本草纲目 ·原序》：“如对冰壶玉鉴，毛发可指数也。”

指数Index

一种表明社会经济现象动态的相对数。运用指数可以测定不能直接相加和不能直接对比的社会经济现象的总动态，分析社会经济现象总变动中各因素变动的影响程度，以及研究总平均指标变动中各组标志水平和总体结构变动的作用。按所反映的现象范围不同，指数分为个体指数和总指数。个体指数反映个体经济现象变动的相对数，如个别产品的物量指数、个别商品的价格指数等；总指数反映全部经济现象变动的相对数，如工业总产值指数、居民消费价格总指数。按所反映的现象性质的不同，分为数量指数和质量指数。数量指数反映生产、经营或经济活动数量的变动，如商品销售量指数；质量指数反映经济活动质量的变动，如产品成本指数、劳动生产率指数等。

指数

测定一种变量在时间上或空间上变动程度的相对数。测定一种经济指标在时间上或空间上变动程度的相对数，称为“经济指数”。按照测定对象的范围，可分为个体指数和总指数；按照经济指标的性质，可分为数量指数和质量指数；按照基期的不同，可分为定基指数和环比指数；按照计算时选择的同度量加权因素的不同，可分为拉氏指数和派氏指数(后者又称“帕氏指数”)等。

指数

用来测定一个变量对于一个特定的变量值大小的相对数。它用来反映不能直接加减的单位所组成的复杂现象总体数量上的变动方向和变动程度，分析现象总体变动中各个因素的影响作用，以及通过指数数列进行复杂现象总体长期发展趋势的分析。

指数index

用来测定一个变量对于一个特定的变量值大小的相对数。它用来反映不能直接加减的单位所组成的复杂现象总体数量上的变动方向和变动程度，分析现象总体变动中各个因素的影响作用，以及通过指数数列进行复杂现象总体长期发展趋势的分析。

指数

把数据资料联系起来并对其结果进行综合评价的一种相对数。指数法主要用于分析复杂现象总体综合变动的状况，而复杂现象总体的特点就在于各种事物的度量单位不同，不能直接加总以综合，反映它们的变动。指数的基本作用是：综合反映复杂现象总体总变动的程度和方向；通过指数体系对现象的总变动进行因素分析，分析各个因素对总变动的影响程度和绝对效果。指数具有如下性质：（一）综合性。综合反映同类现象各种事物变化的大小和方向。（二）代表性。在实际编制指数时，只能选取若干重要项目作为代表，不可能将所有项目一一列入计算范围。（三）相对性。指数常以相对数或比率形式出现，表明现象发展变化的程度。（四）平均性。指数所表示的综合变动是多种事物的平均变动，作为任何一种个别事物变动的代表。指数按不同的分类方法可分为：个体指数和总指数、简单指数和加权指数、综合指数和平均指数、数量指标指数和质量指标指数、动态指数和静态指数、定基指数和环比指数。

指数

反映事物或现象变动程度的一种相对数。

指数Index

是一种综合指标，用以描述一组不同的但又有联系的变量的总的变化水平，从而能对这组变量在不同时期或不同场合所处的水平作出比较。指数的种类很多，但常用的是数量指数(quantity index) 和价格指数(price index)。下面分别介绍这两个指数。设P为价格向量，X为消费品向量：
P⁰＝(p₁⁰,p₂⁰，……p_i⁰，……p_n⁰)
X⁰＝(x₁⁰,x₂⁰，……x_i⁰，……x_n⁰)
P¹＝(p₁¹,p₂¹，……p_i¹，……p_n¹)
X¹＝(x₁¹,x₂¹，……X_i¹，……x_n¹)
其中，上标表示时期，0为第0期 （基期）,1为第一期，下标表示商品。
1.数量指数
指反映某些数量指标的变化水平的相对数。如反映居民实际收入变化水平的指数。反映某种产品产量增长水平的指数。计算指数时需要对数据资料进行加权平均。数量指数的计算是以价格作为权数的，根据选择权数时期的不同，数量指数又分为两类：
(1) 拉斯贝耶斯数量指数 (Laspeyres Quantity Index)，它是以基期的价格作为权数的，其计算公式为：

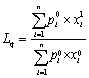
(2)帕舍数量指数(Paasche Quantity Index)，它是以第一期的价格作为权数的，其计算公式为：

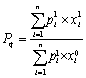
2.价格指数
是比较一组价格在不同时期或地区的总水平变动的相对数。它是以数量指标作为权数的。与数量指数一样，根据所选择的权数的时期的不同，也有两种价格指数：
(1) 拉斯贝耶斯价格指数 (Laspeyres Price Index)，它是以基期的数量指标作为权数的。其计算公式为：

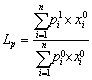
(2) 帕舍价格指数 (Paasche Price Index)，它是以第一期的数量指标作为权数的。其计算公式为：

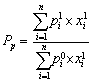
从上面的介绍可以看出，不管是对于数量指数还是价格指数，拉斯贝耶斯指数和帕舍指数的区别在于前者以基期指标为权数，而后者以第一期指标为权数。但两者的区别并不尽限于此，事实上这两种指数提供的信息并不相同，相应用于不同的分析目的 (H·范里安，1995,P.166～171)。而且它们都存在着一定的缺陷，还有待于改进。

指数

一种表明社会经济现象变动程度的相对数。广义的指数包括表明简单总体（数量可以直接加总的社会经济现象的总体）变动程度的相对数和表明复杂总体（数量不能直接加总的社会经济现象的总体）变动程度的相对数。狭义的指数只指专门用以表明复杂总体综合变动程度的特殊相对数。指数按其所反映对象范围不同分为个体指数和总指数，按其反映现象的性质不同分为质量指标指数和数量指标指数，按其采用的基期不同分为定基指数和环比指数。指数的作用：
❶用来测定不能直接相加和直接对比的社会经济现象的动态：
❷可以测定某一社会经济现象总变化受各因素变动的影响程度；
❸可以测定平均数对比中各因素的影响。

指数index

❶表示一个数自乘若干次的数字，记在数的右上角，例如3²,4³,6ⁿ，右角上的小数字2,3,n。
❷根据所测量值以表示不能精确测定值的公式。如心指数^*。

---

指数index

表明同类脑波在单位时间内出现的多寡用指数表示之，即纸速在3cm/s时，100cm内某一种脑波出现的厘米数，用%表示之，例如在100cm内某一脑波出现达40cm，则称该波的指数为40%。

指数index number

计量一种或多种变量在时间上（或空间上）变动程度的相对数。主要用于比较同类经济现象在时间上的相对变动（如不同时期商品价格的变动）；这时作为比较标准的时期称为基期，并以基期的指数为100来表明其他时期与基期相比的相对变动；也用于比较经济现象在空间上的相对变动（如比较不同地区的工资水平），这时以某地区作100来表明其他地区与这个地区相比的相对变动。指数一般用于综合多种不能直接相加的现象，反映其总的变动程度。
指数按所研究现象范围的不同，可分为个体指数和总指数。总指数按计算形式的不同，又可分为综合指数和平均数指数。指数按加权与否，还可分为简单指数（不加权指数）和加权指数。权数是对各个变量具有权衡轻重作用的数值，总指数所包含的各种物品的重要性各不相同，如不加权，则各种物品在指数中的重要性，就无法表示出来。
加权指数，又可分为基期加权指数和计算期加权指数。现以物价指数为例，加以说明。
(1)基期加权物价指数，是以基期销售量为权数的加权物价指数。这种指数是德国人拉斯拜尔(E.Laspeyres)1864年提出的，简称拉氏物价指数或拉斯拜尔公式(Laspeyres’Formula)。公式如下：

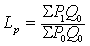
上式中，L_p为拉氏物价指数，Q为基期销售量，P₀和P₁分别为基期和计算期的价格。
(2)计算期加权物价指数，是以计算期销售量为权数的物价指数。这种指数是德国人帕舍(H.Paasche)1874年提出来的。简称帕氏物价指数或帕舍公式(Paasche’s Formula)。公式如下：

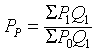
上式中，P_p为帕氏物价指数，Q₁为计算期销售量，P₀和P₁分别为基期和计算期的价格。
美国统计学家费雪(I.Fisher)1922年从大量的指数公式中筛选出一种计算指数的理想公式(ideal formula)。理想公式实际上是拉斯拜尔公式与帕舍公式的几何平均数。物价指数的理想公式(F_p)为：

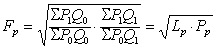
这个公式能满足时间互换测验(原来指数与基期、计算期互换后的指数之乘积是否等于1的测验)和因子互换测验(原来物价指数与价、量互换后所得的物量指数之乘积是否等于价值指数的测验)，费雪认为是最佳公式，故命名为“理想公式”。这个公式的主要优点在于能够使拉氏指数和帕氏指数所具有的方向相反的偏误相互抵消，具有一定的学术价值。但计算过于复杂，实际工作中很少应用。
由于基期权数资料比计算期权数资料容易取得，西方国家最常用的经济指数公式，多为拉氏加权综合公式及其修改后的固定加权算术平均数公式。

上式左方为拉氏加权综合公式；右方为修改后的加权算术平均数公式，它是拉氏加权综合公式的变形。对加权算术平均数公式的权数多采用固定权数，它可以是基期权数，也可以是某时期的固定权数。为了使固定权数代表的属性不致于和计算期权数的实际属性差别过大，权数大都每隔若干年(例如5年)调整一次。

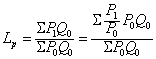
指数

exponent;index

指数

index;index number
成本～cost index;index of working cost/出口商品价格～index number of the prices of export products /道琼斯股票～ Dow Jones Index/工资～index number of wages;wage index/商业～index of business /购买力～purchasing power index/国内生产总值～index number of gross domestic production(GDP)/国民生产总值～ index number of gross national production/国际标准～international standard index/结构～structural index/劳动生产率～index number (or index)of labor productivity/生产～ index of production/生活费～ cost of living index /稳定～index of stability/消费物价～consumer price index (CPI)/综合～ composite index /总～general index;summary index;group index /～变化index movement /～法index method/～化indexation/～化制度indexation system/～律index law/～体系index system/～系列index series