抽样误差chōu yàng wù chāошбка вборки

抽样误差sampling error

又称代表性误差。统计学上指样本统计数与总体参数间的差异。抽样误差小，统计数可以较好地作为总体参数的估计值；抽样误差大，则统计数不能代表总体参数。如果对总体变异情况有较多了解，并运用适当抽样方法，尽量增加样本容量及有效控制试验条件，均可降低抽样误差。

抽样误差

按随机原则抽样，所得抽样指标与总体指标的差数。包括抽样平均数与全及平均数的差数，即抽样平均误差；抽样成数与全及成数的差数。

抽样误差sampling error

指在抽样研究过程中，由于偶然的机遇而造成的误差。主要是指抽取样本的统计量与总体参数之间的误差。表示抽样误差大小的指标为标准误，计算公式为：

式中S_为标准误，S为标准差，n为样本含量。抽样误差的分布符合正态分布规律者，均运用这一规律对抽样误差进行检验，用来判定误差的性质，即是否来自抽样误差。

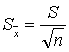
抽样误差Sampling Error

衡量抽样检查准确程度的指标。按随机原则抽样时，在没有登记误差和系统性误差的条件下，由不同的随机样本得出不同估计量而产生的误差。分为抽样平均误差和抽样极限误差。抽样误差越大，表明抽样总体对总体的代表性越小，抽样检查的结果越不可靠。反之，抽样误差越小，说明抽样总体对总体的代表性越大，抽样检查的结果越准确可靠。

抽样误差

也称代表性误差。是指在严格按照随机原则抽样时，所得样本指标与总体指标的差值。主要是样本平均数与总体平均数，样本成数与总体成数的差值。抽样误差是抽样调查所固有的，是没有确定原因的随机性误差，是衡量抽样调查准确性的指标。抽样误差的大小主要受以下三个因素的影响：(1) 样本单位数的多少。在一定的抽样方式下，样本数目越多，抽样误差越小，反之，抽样误差越大。如果样本单位数与全及总体单位数相等时，抽样调查就等于全面调查，也就不存在抽样误差了。(2)被研究总体的标志变异程度。标志变异程度越大，抽样误差越大，反之，抽样误差越小。如果总体中各单位的标志值都相等，没有差异，则抽样指标与全及指标相等，抽样误差也就不存在了。(3)抽样调查的组织方式。如在同样条件下，不重复抽样比重复抽样的抽样误差小，在总体现象分类比较明显时，分层抽样比其他方式的抽样误差小。抽样误差的计算，由于总体真正的参数值未知，真正的抽样误差也未知，因此，一般都以抽样平均误差来代替真正的抽样误差。抽样平均误差是指所有可能出现的样本统计值的标准差。通常，运用最多的抽样平均误差是指样本平均数或样本成数的标准差。计算公式分别为：

式中，μx代表样本平均数的平均抽样误差，δ为总体标准差，n为样本单位数；

式中，μp代表样本成数的平均抽样误差，p为总体成数，n为样本单位数。上述两个公式中的总体标准差δ与总体成数p是未知的，因此，实际计算时，则以样本标准差代表总体标准差，以样本成数代替总体成数

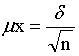
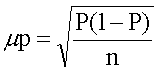
抽样误差

按随机原则抽样时，在没有登记误差和系统性误差的条件下，单纯由于不同的随机样本得出不同估计量而产生的误差。这种误差是抽样调查所不可避免的，可运用大数定律的数学公式加以精确计算，确定它具体的数量界限，并通过抽样设计程序加以控制。抽样单位数的多少，总体被研究标志的变异程度，都会影响抽样误差。

抽样误差sampling error

按随机原则抽样时，在没有登记误差和系统性误差的条件下，单纯由于不同的随机样本得出不同的估计量而产生的误差。这种误差是抽样调查所不可避免的，可运用大数定律的数学公式加以精确计算，确定它具体的数量界限，并通过抽样设计程序加以控制。抽样单位数的多少，总体被研究标志的变异程度，都会影响抽样误差。

抽样误差

由于抽样的随机性而产生的样本指标与总体指标之间的差值。抽样调查是从总体中抽查部分单位，即使严格遵守随机原则，也不可能使样本结构与总体结构完全一致，因而，这种误差是不可避免的。抽样设计的任务就是使它缩小到最低限度，或把它控制在可允许的范围之内。抽样误差作为一项调查评测指标，其作用在于说明样本对总体的代表性的大小。抽样误差愈小，表明样本对总体的代表性就愈高；反之，则代表性就愈低。抽样误差的大小，主要受下列三个因素的影响：（一）样本单位数目的多少。在其他条件不变的情况下，抽取的样本单位数愈多，抽样误差就愈小；反之，则抽样误差愈大。（二）总体的标志变异程度。在其他条件不变的情况下，总体的标志变异程度愈小，抽样误差就愈小；反之，则抽样误差就愈大。（三）抽样方法的不同。如在其他条件相同的情况下，分层抽样所取得的样本就比简单随机抽样的抽样误差要小一些。
在抽样调查中，无论采取哪种抽样方法都会产生误差。一般误差有两种：一种是抽样时违反了随机的原则或由于登记过录及计算错误引起的系统性误差。另一种则是由于偶然因素的影响。即使遵守了随机的原则，也要产生偶然的误差。从理论上讲，前一种误差在实际操作中是可以避免的。而后一种误差由于是采取随机抽样的方法时所产生的，所以是不可避免的(因为只要是采取随机原则抽样，就一定会出现样本和总体之间的误差)。计算抽样误差的意义在于：说明样本代表性是否充分。如果计算的抽样误差大，说明样本对总体的代表性差，抽样准确率低。抽样误差小，说明样本对总体的代表性强，则抽样的准确率就高。抽样误差是不能够直接计算出来的。但是，根据数理统计的原理，抽样误差可以用抽样的平均误差来代替。在受众和舆论调查中，由于较多的是调查被访者对某些问题的赞成或反对的态度，所以，一般多用比率抽样平均误差来计算抽样平均误差。

抽样误差

抽样总体得到的指标数值与全及总体的指标数值之间的差别。包括具体样本指标与总体指标的实际误差以及所有样本指标与总体指标之间的平均离差两种。后者主要有抽样平均数与全及平均数之差，抽样成数与全及成数之差。有抽样调查，就有抽样误差存在，其作用主要是说明样本指标代表性的大小及样本指标与总体指标相差的一般范围。抽样误差愈大，表示样本的代表性愈小。影响抽样误差大小的主要因素有：
❶抽样单位数的多少；
❷全及总体的标志变动程度；
❸抽样调查的组织形式及抽选样本的方法。

抽样误差

亦称“代表性误差”。指随机抽样调查所取得的抽样指标与全及指标的差数。主要是抽样平均数与全及平均数的差数，抽样成数与全及成数的差数。抽样误差仅指由于样本不足以代表总体所产生的误差，不包括由于记录、谎报等登记错误所产生的误差。抽样误差的大小主要受以下三个因素的影响：(1) 样本单位数目的多少。在一定抽样条件下，样本单位数目愈多，抽样误差愈小； 反之愈大。如果把样本单位数目扩大到包括全及总体所有单位时，就不存在抽样误差了。(2) 被研究总体的标志变异程度。标志变异程度愈大，抽样误差愈大； 反之愈小。如果总体各单位的标志值没有差异，也就没有抽样误差了。(3) 抽样调查的组织方式和抽选方法，对抽样误差的大小也有很大影响。在一个全及总体中，可以抽取很多样本，由所有可能出现的样本计算的抽样指标都存在抽样误差，其大小和正负偏向各不相同，它们的平均数 （平方平均数） 就叫做抽样平均误差，用符号μ来表示。它表示的是一个可能的误差范围，而不是确切的误差数值。抽样调查的结果，实际误差落在正负平均误差范围之内的概率符合大数定律的正态分布定理： 调查结果在正负一个平均误差范围内的概率为68.27%; 在正负两个平均误差范围内的概率为95.45%; 在三个平均误差范围内的概率为99.73%……。

抽样误差

sampling error

抽样误差sampling error

由于抽样而引起的总体指标（参数）与样本指标（统计数）之间的差异。在抽样调查中，不论用何种抽样方法，从总体中抽取样本进行研究，都不会与总体结果完全一致。即使在抽样过程中，执行随机原则非常严格，根据样本计算出来的平均数()与总体平均数(μ)也不会完全相等。假如进行多次重复抽样，求得的各样本平均数总是在总体平均数上下浮动。其他统计指标如标准差等，也是如此。这种由于抽样而引起的总体指标与样本指标之间的差异，叫做抽样误差。抽样误差的大小，与样本能够代表总体的真实性恰好成反比关系。抽样误差越大，样本代表总体的真实性越小，反之，抽样误差越小，样本代表性就越大。