抛物线的标准方程paowuxian de biaozhun fangcheng

取经过焦点F且垂直于准线l(交点为K)的直线为X轴，线段FK的垂直平分线为Y轴建立平面直角坐标系(如图1)，设|FK|=p，则由|MF|=d导出的方程y²＝2px，叫做抛物线的标准方程，它的焦点是F(p/2,0)，准线是l:x=-p/2.

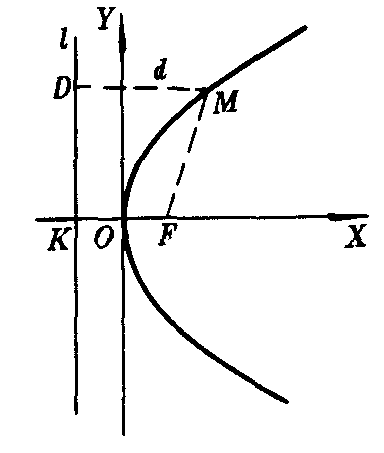
图1

这一标准方程的导出过程表明“抛物线上任意一点的坐标都适合这一方程”，而“坐标适合这一方程的点必在抛物线上”.
由于抛物线和坐标系的不同位置关系，抛物线的标准方程还有：
y²＝-2px(p>0)，焦点F(-p/2,0)，准线l:x=p/2;(如图2);
x²＝2py,(p>0)，焦点F(0,p/2)，准线l:y=-p/2;(如图3);
x²＝-2py(p>0)，焦点F(0,-p/2).准线l:y=p/2.(如图4).

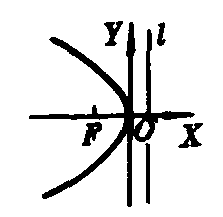
图2

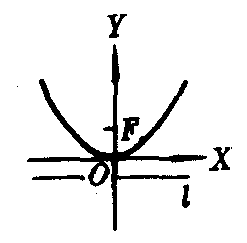
图3

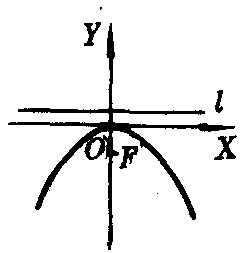
图4

抛物线的标准方程的特征是：
❶左端只含有x²项或y²项，系数是1；右端只含有y或x的一次项，系数可正可负，系数的符号表示抛物线的开口方向.
❷抛物线的顶点在原点，焦点在坐标轴上，准线垂直于焦点所在的坐标轴.
顶点在点(x₀,y₀)，准线垂直于坐标轴的抛物线方程如下表所示(其中p>0).

方 程	焦 点	准 线
(y-y0)2=2p(x-x0)	(x0+p/2,y0)	x=x0-p/2
(y-y0)2=-2p(x-x0)	(x0-p/2,y0)	x=x0+p/2
(x-x0)2=2p(y-y0)	(x0,y0+p/2)	y=y0-p/2
(x-x0)2=-2p(y-y0)	(x0,y0-p/2)	y=y0+p/2

这些抛物线的方程是利用坐标轴的平移公式由抛物线的标准方程导出的，与标准方程有类似的特征.