抛物线的切线和法线
抛物线的切线和法线paowuxian de quexian he faxian
抛物线y2=2px过切点(x1,y1)的切线方程是y1y=p(x+x1),法线方程是y1x+py=py1+x1y1.
抛物线y2=2px的已知斜率为k的切线方程是y=kx+p/(2k),其中k≠0,平行于抛物线轴的直线和抛物线有且仅有一个公共点,但不是抛物线的切线.
抛物线的切线和法线的性质:抛物线的切线和过切点的焦点半径及直径所成的角相等,并且一切平行于切线的弦都被过切点的直径所平分;抛物线的法线平分过切点的焦点半径和直径的夹角(如图1).
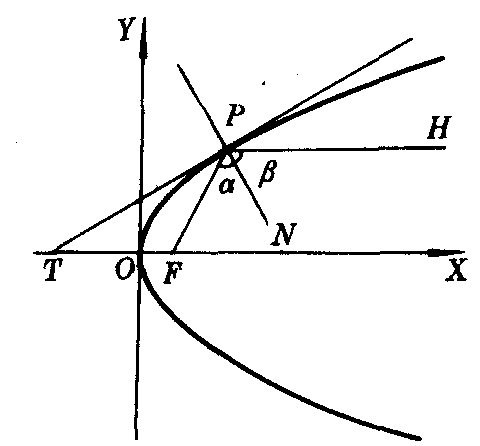
图1
由此可知,抛物线的光学性质是:将抛物线绕轴旋转一周生成旋转抛物面,从焦点发出的光线投射到曲面上,经过曲面反射后,变成平行光线(如图2).反之,把平行于轴的光线投射到曲面上,经过曲面反射后,光线集中于焦点(如图3).
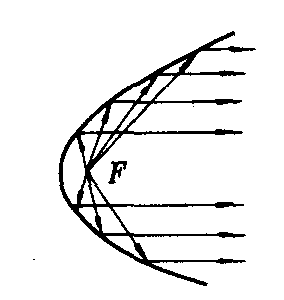
图2

图3
探照灯,太阳灶,抛物面天线都是应用这一性质设计的.
☚ 抛物线的画法 抛物线的切点弦 ☛
- 存亡绝续是什么意思
- 存亡继绝是什么意思
- 存亡继绝是什么意思
- 存人编是什么意思
- 存介堂集帖是什么意思
- 存信篇是什么意思
- 存储是什么意思
- 存储器是什么意思
- 存储器是什么意思
- 存储器是什么意思
- 存储容量模型是什么意思
- 存储模型是什么意思
- 存储费用是什么意思
- 存十一于千百是什么意思
- 存古约言是什么意思
- 存吾文集是什么意思
- 存命汤是什么意思
- 存命汤是什么意思
- 存国、定民之道是什么意思
- 存在是什么意思
- 存在是什么意思
- 存在是什么意思
- 存在是什么意思
- 存在是什么意思
- 存在是什么意思
- 存在·空间·建筑是什么意思
- 存在 消失是什么意思
- 存在与存在者是什么意思
- 存在与时间是什么意思
- 存在与时间是什么意思
- 存在与时间是什么意思
- 存在与虚无是什么意思
- 存在与虚无是什么意思
- 存在与虚无是什么意思
- 存在与虚无是什么意思
- 存在与虚空是什么意思
- 存在(中世纪)是什么意思
- 存在主义是什么意思
- 存在主义是什么意思
- 存在主义是什么意思
- 存在主义是什么意思
- 存在主义是什么意思
- 存在主义是什么意思
- 存在主义是什么意思
- 存在主义是什么意思
- 存在主义是什么意思
- 存在主义是什么意思
- 存在主义是什么意思
- 存在主义是什么意思
- 存在主义是什么意思
- 存在主义、实在论的经验主义和唯物主义是什么意思
- 存在主义哲学是什么意思
- 存在主义哲学是什么意思
- 存在主义心理学是什么意思
- 存在主义教育是什么意思
- 存在主义教育是什么意思
- 存在主义文学是什么意思
- 存在主义文学是什么意思
- 存在主义文学是什么意思
- 存在主义是一种人道主义是什么意思