惠更斯—菲涅耳原理huigengsi—feinieer yuanli

处理光的衍射问题的基本原理。可表述为：行进中的光波波阵面上各面元所发出的子波是相干波，同时传到空间某点时，其总振幅是这些子波的干涉结果。1690年提出的惠更斯原理，可以解决光波的传播方向问题，但无法给出各方向上波的振幅与位相。当时是以牛顿为代表的光的微粒说占上风，由于牛顿的威望，光的波动理论长期没有什么发展。直到19世纪初，杨氏用波的叠加原理解释了薄膜的彩色现象，首先提出“干涉”一词来概括波与波之间的相互作用。菲涅耳继承了惠更斯关于波阵面与子波的概念，并吸收了杨氏关于干涉的思想，对惠更斯原理做了重要补充，发展成为惠更斯—菲涅耳原理。菲涅耳在1815年送交巴黎科学院的第一篇关于衍射的论文中，首次提出了惠更斯—菲涅耳原理。在定量计算中，引入了倾斜因子，解决了几个典型的衍射问题。
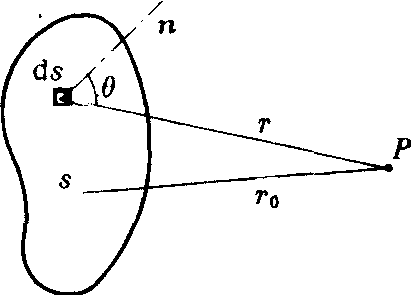
根据惠更斯—菲涅耳原理，设有一任意波阵面S（如图），在其前方任一点P的总振幅是此波阵面上所有小面元ds在P点所生振幅的叠加。对于给定的某面元ds，它在P点所产生的振动的振幅应正比于元面积ds，反比于ds到P的距离r，并与面元ds对P点的倾角有关；而位相由面元ds的初位相和距离r决定。即面元ds在P点所生振动可表为，

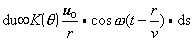
K(θ)即菲涅耳引入的倾斜因子，θ是面元ds与r之间的夹角，θ=0时，K(θ)=1,θ逐渐增大，K(θ)逐渐减小，θ≥π/2时，K(θ)=0;u0是次波源处原波的振幅；v是波速。故波阵面S在P点所产生的总振动为

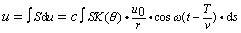
c是比例系数。只要算出此积分，衍射问题就可获得定量解决。该积分的计算比较困难，但在某些有对称性的简单情形可很好解决。菲涅耳为了应用惠更斯-菲涅耳原理定量解决这类衍射问题，提出了菲涅耳半波带法，且其计算与实验结果相符。他的成就得到了人们公认，至今惠更斯—菲涅耳原理仍是波动光学的一个基本原理，是解决衍射问题的基础。