中位数

---

将总体单位的某一数量标志的各个数值按大小顺序排列，居于中间位置的那个数值就是中位数。

中位数也是一种代表值，可以代替算术平均数来反映某种现象的一般水平。

中位数的计算方法，要根据所掌握的资料而定，一般可分为两种情况：一是资料未经分组；二是资料已经分组。

1．在资料未分组时确定中位数的方法。

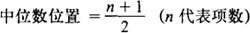
如果总体单位的项数是奇数，则居中间位置的那个标志值就是中位数。

假设有7个工人生产某种产品，他们的日产量(件)按顺序排列是：4、4、6、8、9、12、14、。则：

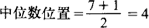，即第四个工人的日产量8件为

中位数。

如果总体单位数是偶数，则中间位置的两个标志值的算术平均数为中位数。

假设上例资料为8人，另一工人的产量为15。则：中位数位置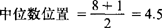

中位数的第四和第五个工人的日产量的算术平均数，即(8+9)÷2=8．5(件)。

2．在资料已分组情况下确定中位数的方法。

在组距数列条件下确定中位数，按下列步骤进行。

第一步，确定中位数所在组。

把整个数列中的总体单位数(或总次数)除以2。

第二步，按照下限公式或上限公式确定中位数的近似值。

下限公式为：

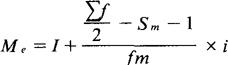
式中：

M_e代表中位数；

I代表中位数所在组的下限；

fm代表中位数所在组的次数；

S_m－1代表中位数所在组以下的累计次数；

∑f代表总次数；

i代表中位数所在组的组距。

上限公式为：

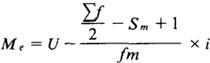
式中：

U代表中位数所在组的上限；

S_m+1代表中位数所在组以上的累计次数。

下限公式和上限公式，都是以中位数所在组内的次数均匀分配为前提的，用这两个公式计算的数值只是中位数的近似值。

例如，某地农户年收入情况如下表：

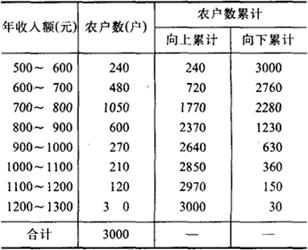
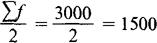
中位数在第三组内。

从表中资料可知：

L=700 fm=1050 u=800

i=100 S_m－1=720 S_m+1=1230

按下限公式计算中位数：

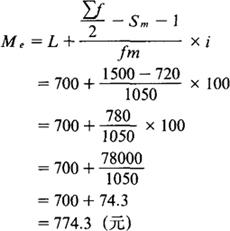
按上限公式计算中位数：

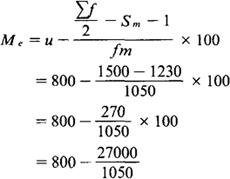
=800－25．7=774．3(元)