两条异面直线的公垂线在这两条异面直线间的线段的长,叫做两条异面直线的距离.
例 空间四边形ABCD,连结对角线AC和BD,E,F分别是BC,AD中点,AB=BC=CD=DA=AC=BD,如图(1)求证:EF是异面直线BC,AD的公垂线.
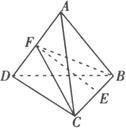
(2)设AB=a,求异面直线BC,AD间的距离.
策略 欲证EF是异面直线BC,AD的公垂线,已知EF与它们都相交,只要证EF与它们都垂直即可,这可通过已知条件构造等腰三角形即可实现.
证明 (1)连结FB,FC.
∵AB=BC=CD=DA=BD=AC,
∴△ABD≌△ADC且为等边三角形.
∵F为AD中点,
∴CF=FB(全等三角形的中线长相等),
则△FBC为等腰三角形,E为底边BC的中点,
∴EF⊥BC.
连结EA,ED,同理可证EF⊥AD,
又∵EF与AD,BC都相交,∴EF是AD,BC的公垂线.
(2)由(1)的证明知EF是AD、BC的公垂线.
∴EF的长就是这两条异面直线间的距离.
∵AB=a,在等腰△FBC中,FB=FC=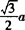 ,
,
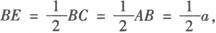
在Rt△BEF中,
EF2=BF2—BE2
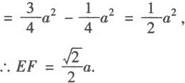
即异面直线BC,AD间的距离为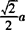 .
.
点评 证明一条线段是异面直线的公垂线时要注意证明两点:
❶ 垂直;
❷ 相交.
- 蠮是什么意思
- 蠮螉是什么意思
- 蠮螉塞是什么意思
- 蠮螉窠是什么意思
- 蠯是什么意思
- 蠯脂是什么意思
- 蠰是什么意思
- 蠰溪是什么意思
- 蠰虫是什么意思
- 蠰蟲是什么意思
- 蠰谿是什么意思
- 蠱是什么意思
- 蠱媚是什么意思
- 蠱毒犀是什么意思
- 蠱蟲是什么意思
- 蠲是什么意思
- 蠲丁是什么意思
- 蠲体祈祷是什么意思
- 蠲免是什么意思
- 蠲免汰除是什么意思
- 蠲减是什么意思
- 蠲削是什么意思
- 蠲削烦苛是什么意思
- 蠲化是什么意思
- 蠲去是什么意思
- 蠲叟是什么意思
- 蠲复是什么意思
- 蠲宥是什么意思
- 蠲容是什么意思
- 蠲平是什么意思
- 蠲弃是什么意思
- 蠲弛是什么意思
- 蠲忙是什么意思
- 蠲忧是什么意思
- 蠲忿是什么意思
- 蠲忿犀是什么意思
- 蠲恤是什么意思
- 蠲振是什么意思
- 蠲放是什么意思
- 蠲放赦释是什么意思
- 蠲救是什么意思
- 蠲敝崇善是什么意思
- 蠲斋是什么意思
- 蠲櫘瘗骼是什么意思
- 蠲欠是什么意思
- 蠲毒饮是什么意思
- 蠲汰是什么意思
- 蠲洁是什么意思
- 蠲浊流清是什么意思
- 蠲浊流清,废贪而立廉。是什么意思
- 蠲浊而流清,废贪而立廉。是什么意思
- 蠲涤是什么意思
- 蠲渴疾是什么意思
- 蠲烦是什么意思
- 蠲略是什么意思
- 蠲疏是什么意思
- 蠲疴是什么意思
- 蠲疾是什么意思
- 蠲痛丸是什么意思
- 蠲痛五汁膏是什么意思