定理1 如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行,用符号表示为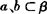 ,a∩b=A,a∥α,
,a∩b=A,a∥α,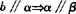 .
.
定理2 垂直于同一条直线的两个平面平行,用符号表示为
α⊥a,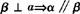 .
.
例1 平行于同一平面的两个平面平行.
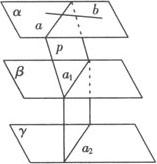
已知:如图所示三个不同平面α、β、γ中α∥β、β∥γ,求证:α∥γ.
策略 判定两平面平行,常用途径有:
(1)证明其中一个平面内有两条相交直线平行于另一个平面;
(2)证明两个平面同垂直于一条直线,这里两条途径都可.
证法一 在α内取两条相交直线a和b,过a作平面p交β于a1.
∵α∥β,
∴a∥a1,又过a1作平面q交γ于a2.
∵β∥y,
∴a1∥a2,故a∥a2,又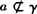 ,
,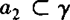 ,
,
∴a∥γ,
同理可证b∥γ,又a与b相交,
∴α∥γ.
证法二 作直线l⊥α,
∵α∥β,
∴l⊥β,又β∥γ,
∴l⊥γ,由l⊥α,l⊥γ,
∴α∥γ.
点评 本题考查平面与平面平行的判定问题,涉及到的两种思考途径是基本的方法,应力求掌握,其基本思路为:
线线平行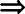 线面平行
线面平行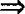 面面平行.
面面平行.
线线垂直 线面垂直
线面垂直 面面平行.
面面平行.
例2 正方体ABCD—A1B1C1D1中,E、F分别是CC1、AA1的中点,求证:平面BDE∥平面B1D1F.
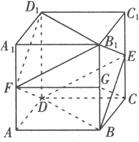
策略 要证平面BDE∥平面B1D1F,区为BD∥B1D1,所以只需证明FB1∥DE.
证明 设G是BB1的中点,连结FG、CG.
∵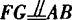 ,
,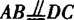 ,∴
,∴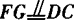 .
.
∴四边形FGCD是平行四边形,则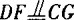 .
.
由题设可得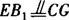 ,则
,则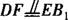 ,所以四边形DFB1E是平行四边形.
,所以四边形DFB1E是平行四边形.
∴B1F∥ED,因为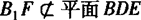 ,
,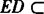 平面BDE,所以B1F∥平面BDE.
平面BDE,所以B1F∥平面BDE.
又∵B1D1.∥BD,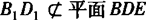 ,BD
,BD 平面BDE.
平面BDE.
∴B1D1∥平面BDE.
∵B1D1∩B1F=B1,∴平面BDE∥平面B1D1F.
点评 证“面面平行”,要先证“线线平行”.进而要证“线面平行”,最后证出面面平行,这就是立体几何中最常用的化归思想(线线、线面及面面的相互化归).本题也可用“垂直”判定,请读者自己探讨.
- 趋翔闲雅是什么意思
- 趋而过庭是什么意思
- 趋职是什么意思
- 趋肤效应是什么意思
- 趋背是什么意思
- 趋舍是什么意思
- 趋舍异路是什么意思
- 趋舍指凑是什么意思
- 趋舍有时是什么意思
- 趋舍有时。是什么意思
- 趋营是什么意思
- 趋行是什么意思
- 趋触性是什么意思
- 趋让是什么意思
- 趋访是什么意思
- 趋诣是什么意思
- 趋谄逢迎是什么意思
- 趋谈是什么意思
- 趋谒是什么意思
- 趋谒参拜是什么意思
- 趋走是什么意思
- 趋走拜谒是什么意思
- 趋走炎热是什么意思
- 趋赴是什么意思
- 趋赴趣向是什么意思
- 趋趄是什么意思
- 趋趋是什么意思
- 趋趋眼是什么意思
- 趋趋蝍蛆是什么意思
- 趋跄是什么意思
- 趋跄跪拜是什么意思
- 趋蹡是什么意思
- 趋蹶是什么意思
- 趋车是什么意思
- 趋辞是什么意思
- 趋辟是什么意思
- 趋过是什么意思
- 趋迎是什么意思
- 趋迓是什么意思
- 趋进是什么意思
- 趋迷眼儿是什么意思
- 趋送是什么意思
- 趋避是什么意思
- 趋避冲突是什么意思
- 趋避式动机冲突是什么意思
- 趋避性是什么意思
- 趋重是什么意思
- 趋锵是什么意思
- 趋阙是什么意思
- 趋附是什么意思
- 趋附奉承是什么意思
- 趋附就是什么意思
- 趋附或归附的人多是什么意思
- 趋附权势是什么意思
- 趋附美色是什么意思
- 趋附者之多是什么意思
- 趋陪是什么意思
- 趋隅是什么意思
- 趋青是什么意思
- 趋风是什么意思