形数form factor

树干材积(V)与树干在X处的比较圆柱体之积之比。形数f_x为树干X处断面积(g_x)和树高(h)的函数，一般表达式为。属干形饱满度指标。形数主要有：
❶胸高形数。取胸高断面为比较圆柱体的横断面的形数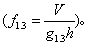是常用的干形指标。当干形饱满度相同时，它受树高的影响不能独立反映干形。它是树高的减函数。
❷正形数。树干材积与树干某一相对高(如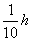)的比较圆柱体的体积之比的形数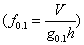。又称标准形数、真形数。它不受树高影响能独立反映干形，但要求测定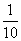树高处直径，实践中很少用来计算立木材积。
❸实验形数。林昌庚提出用比较圆柱体的横断面为胸高断面，其高度为树高加3m的形数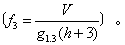它吸取了胸高形数以胸高为测点和正形数能独立反映干形的优点。中国针叶树种的平均实验形数为0.39～0.45，阔叶树为0.4。

形数Xingshu

古希腊的毕达哥拉斯（参见该条）学派认为数是万物的本原，因此极为重视数的理论研究，他们常把数描绘成沙滩上的沙粒或小石子，并由它们排列而成的形状对自然数进行研究。形数就是指平面上各种规则点阵所对应的数， 是毕达哥拉斯学派最早研究的重要内容之一。
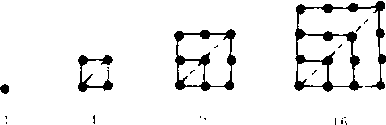
最简单的形数是三角形数， 第n个三角形数 (我们记作p3(n)3即自然数列的前n项和，因为相应个数的点可以排列成正三角形，它们的前几个是一般地有

p3(n)=1+2+3+…+n=1/2n (n+1)

三角形数是研究一般多边形数的基础， 正如任意多边形都可分解为一些三角形， 一般的多边形数也可以分解为一些三角形数之和。
目然数的平方n²称为正方形数， 因为用点表示时它们可以排成正方形， 前几个正方形数是：
第n个正方形数n²恰好是前n个奇数之和

n²＝1+3+5+…+ (2n-1)

据说毕达哥拉斯学派正是用直角曲尺在平面方形点阵上自1开始逐渐向外推移而生成相继的正方形数的，相当于

n²+ (2n+1) = (n+1)²

第n个正方形数n²还可以看作第n-1个三角形数与第n个三角形数之和， 实际上：

如果证n²＝p4(n), 那么上式可写成p3(ⁿ-¹)+p3(ⁿ⁾＝p4(n⁾

行数与列数之差为1的长方形点阵所对应的数称为长方形数， 前几个是
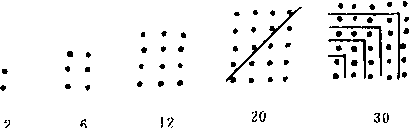
它们是由2开始通过对相继的偶数求和生成的， 第n个长方形数恰好是前n个偶数之和，根据其定义， 第n个长方形数是

n (n+1) =2+4+6+…+2n

毕达哥拉斯学派已经看到， 第n个长方形数是第n个三角形数的2倍。
行数与列数之差大于1的长方形点阵所对应的数被毕达哥拉斯学派称为扁长数， 希腊人后来也不加区别地把扁长数与长方形数统称为长方形数， 或者把一切合数称为平面数， 并且推导出一些有趣而重要的定理。
毕达哥拉斯学派还研究其他多边形数， 如五边形数、六边形数等。如果记第n个五边形数为p5⁽ⁿ⁾，第n

个六边形数为p(n)6, 则

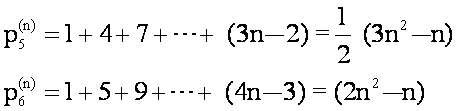
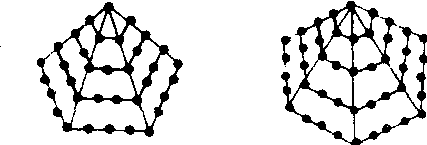
容易看出：
p(n)5=n+3p(n-1)3,p(n)6=n+4p(n-1)3，一般地有：p(^n)m＝n+(m
-2) p(n-1)3, m=3, 4, ……
自毕达哥拉斯学派开创了形数理论之后， 它一直是希腊理论算术（即数论）的重要内容，也常常出现在后世的数论著作中。

形数

树干干形指标之一。即树干材积与比较圆柱体体积（树干上某一固定断面和树高等高的圆柱体体积）之比值。用以反映和研究树干形状及计算树干材积。计算公式为：

树干材积=树高×胸高断面积×形数