异面直线所成的角yimian zhixian suocheng de jiao

a,b是两条异面直线，经过空间任意一点O，作直线a′∥a，直线b′∥b，则直线a′和直线b′所成的锐角（或直角）叫做异面直线a和b所成的角(图1).

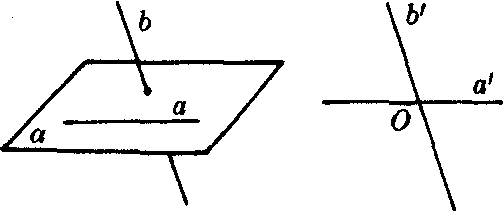
图1

异面直线所成的角反映了两条异面直线在方向上的差异.它是研究两条异面直线互相垂直、三垂线定理的基础.计算异面直线所成的角的基本步骤是：
❶根据异面直线所成的角的定义，找出异面直线所成的角θ.

❷解含有角θ的三角形，求出角θ的大小.
在完成第一步时，应注意为完成第二步作好准备.

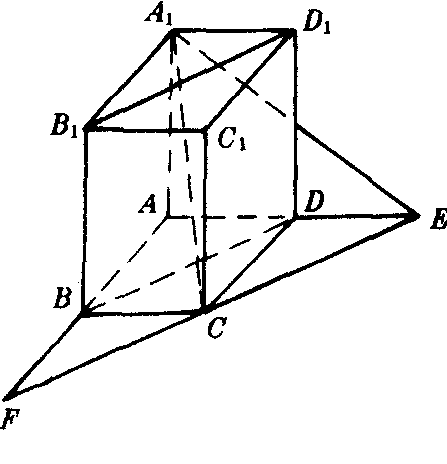
图2

通常把角θ的顶点选在两条异面直线中的一条上.
例 在长方体ABCD-A₁B₁C₁D₁中(图2),BC=a,CD=b,DD₁＝c，且b>a.求异面直线A₁C和B₁D₁所成的角.
解 过C作B₁D₁的平行线EF，与AB,AD的延长线分别交于F,E两点.则∠A₁CE就是异面直线A₁C和B₁D₁所成的角.连结A₁E.因为EF∥B₁D₁，所以EF∥BD.四边形BCED是平行四边形.所以CE=BD=

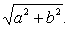
因为

DE=BC=a,

所以

AE=2a.

在Rt△AEA1

中，

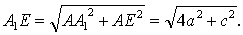
又

A1C=

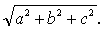
在△A1CE中有

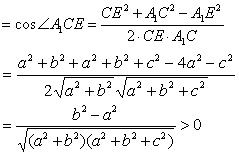
所以A1C和B1D1所成的角为

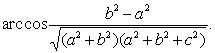
在上面的例题中，若已知a=b，则可根据三垂线定理证明直线A₁C与BD互相垂直，所以A₁C与BD所成的角为90°.这时可不用异面直线所成的角的定义求.