平面图形的面积
平面图形的面积pingmian tuxing de mianji
❶在直角坐标系中计算曲线所围成的平面图形的面积.
若函数f(x),g(x)都是连续的,则曲线y=f (x),y=g (x)与直线x=a,x=b所围成的图形 (见图1)的面积
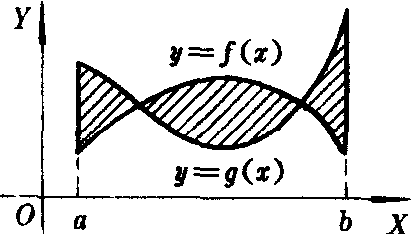
图1
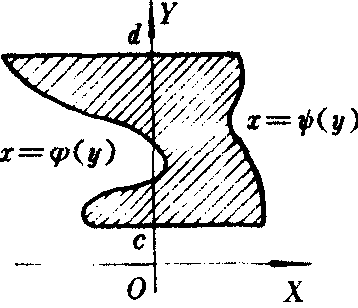
图2
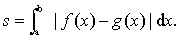
若函数ψ (y) ,ψ (y)都是连续的,则曲线x=ψ(y),x=ψ(y)与直线y=c,y=d的围成的图形(见图2) 的面积
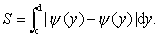
例 求椭圆
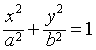 的面积.
的面积.解 由对称性,只需计算椭圆在第一象限这部分的面积S/4,再四倍即可.
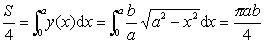
所以X =πab.
❷在极坐标下计算曲线围成的平面图形的面积.
若函数f (θ)在区间 [α,β]上连续,则由极坐标方程r=f (θ),α≤θ≤β表示的曲线与射线θ=α,θ=β (α<β)所围成的平面图形 (见图3) 的面积S=
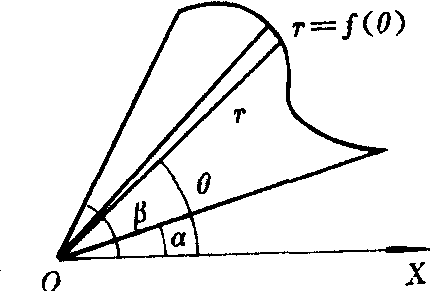
图3
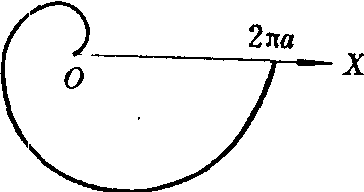
图4
例 求阿基米德螺线r=αθ (0≤θ≤2π)和极轴所围图形的面积,如图4.
解 所求面积
![]()
☚ 定积分的换元积分法 旋转体的体积 ☛
- 敲锣打鼓是什么意思
- 敲锣找孩子——丢人打家伙是什么意思
- 敲锣捉麻雀是什么意思
- 敲锣捉麻雀——不得法是什么意思
- 敲锣掌号是什么意思
- 敲锣放炮是什么意思
- 敲锣的紧跟打鼓的——响(想)到一个点上去了是什么意思
- 敲锣碰到放炮的是什么意思
- 敲锣要敲在锣心上是什么意思
- 敲锣边是什么意思
- 敲锣边儿是什么意思
- 敲镘儿是什么意思
- 敲門石是什么意思
- 敲門磚是什么意思
- 敲门是什么意思
- 敲门僧踏梅花月,入夜猿啼枫树霜。是什么意思
- 敲门声是什么意思
- 敲门打户是什么意思
- 敲门瓦是什么意思
- 敲门石是什么意思
- 敲门砖是什么意思
- 敲门砖,不值钱是什么意思
- 敲门而后入是什么意思
- 敲门问嫁是什么意思
- 敲雷公脑子是什么意思
- 敲顺风锣是什么意思
- 敲骨剥髓是什么意思
- 敲骨取髓是什么意思
- 敲骨吸髓是什么意思
- 敲骨吸髓不吐核是什么意思
- 敲骨吸髓的经济掠夺是什么意思
- 敲骨抽髓是什么意思
- 敲骨榨髓是什么意思
- 敲髓洒膏是什么意思
- 敲鸡牙是什么意思
- 敲麻糖是什么意思
- 敲鼓是什么意思
- 敲鼓敲锣是什么意思
- 敲(俏)皮是什么意思
- 敲𢽴是什么意思
- 敲𩙯是什么意思
- 敲売是什么意思
- 敳是什么意思
- 整是什么意思
- 整䠙皮是什么意思
- 整一个月是什么意思
- 整七里寸是什么意思
- 整不住是什么意思
- 整不出子丑寅卯是什么意思
- 整不出里表是什么意思
- 整丝儿是什么意思
- 整丝工是什么意思
- 整严是什么意思
- 整个是什么意思
- 整个一生是什么意思
- 整个世界是什么意思
- 整个东西是什么意思
- 整个中国是什么意思
- 整个事物中很小的一部分是什么意思
- 整个人开始方了是什么意思