平方根纸的应用

平方根纸又称二项概率纸或统计分析纸。它以几何图的点、直线和圆作图解代替计算，进行统计分析，可用于解决某些参数估计、假设检验、样本含量估计等问题。直观、简便、快速，但数值大时不够精确。
图纸的构造：
(1)平方根刻度：从原点起，横轴和纵轴均以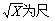度而标以X，如将1标于
(2) 四分圆： 以原点为圆心，取通过点(0,100)和点(100,0)的四分之一圆。
(3) 弧度刻度： 将四分圆的弧度标于图的上周边和右周边。
(4) σ 尺与α尺： 在图纸上端中央，线上为σ尺，1σ的长度等于纵轴或横轴0与1间距的1/2，相当实测点在圆周上分布的标准差。上端左侧是放大为σ的尺，右侧是缩小为σ/的尺，均作为图纸内距离的比较标准。σ尺线下是其单侧概率值α(%)，如从0到1.96σ的距离，α的刻度为2.5%，记为u_0.025。

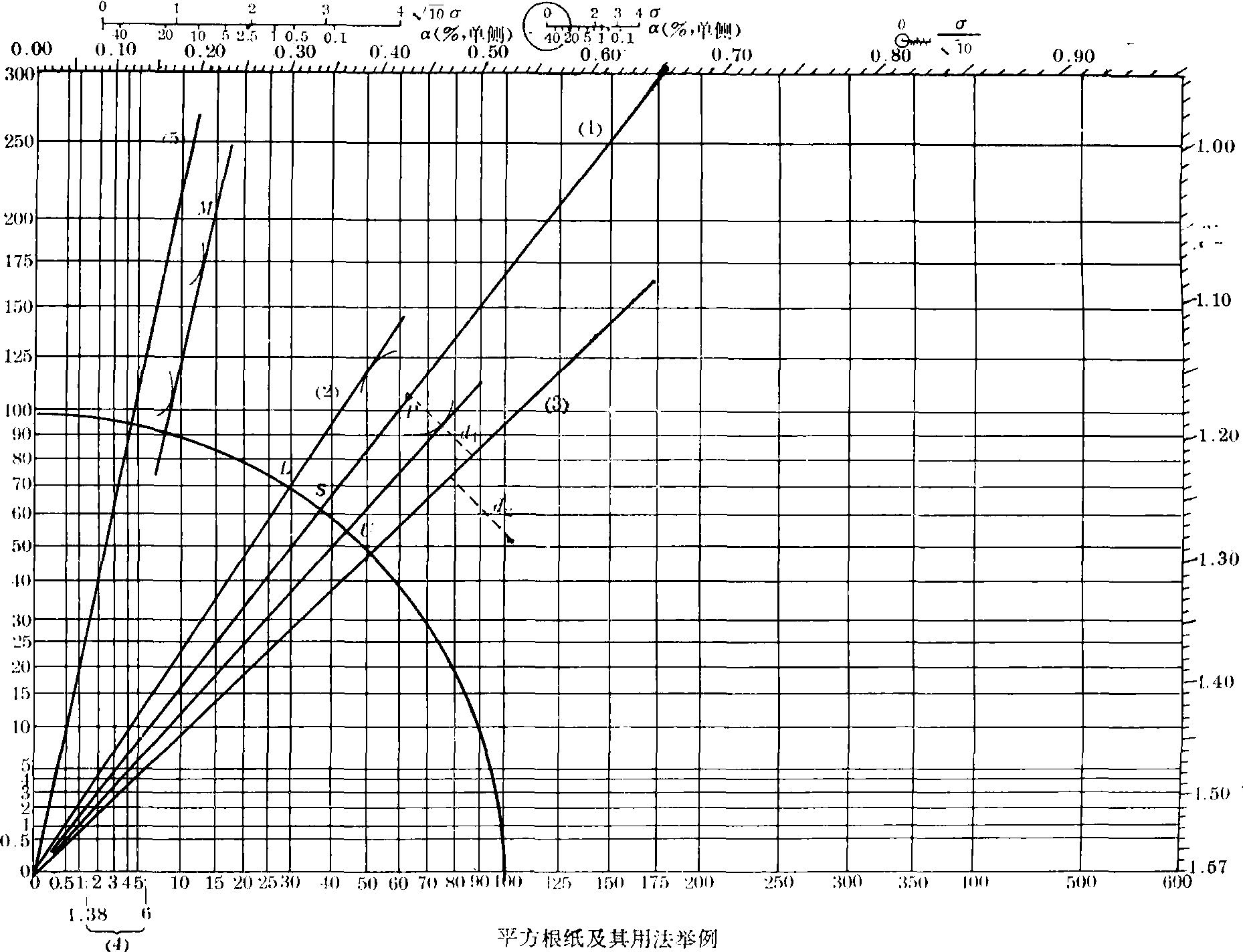
平方根纸的用途很多，如：
❶求总体均数、百分率的可信区间；
❷作假设检验：用u检验、F检验、符号检验、极差检验等比较两个样本率、多个样本率或样本均数；
❸估计样本含量，如已知总体或样本率，欲使样本中含某属性的个体数为c时，应取的样本含量。举例说明用法如下（依例号见图）。
例1 用甲疗法治某病172例，治愈62例，未愈110例。求治愈率及其平方根的反正弦变换值。
过原点O(0,0)及点P(62,110)作直线，称为分割线。线上任一点(X,Y)，其X:Y=62:110，称为分割比。直线交四分圆于点S,S的横坐标36%即所求治愈率(因为62:OP=36:100)。延长OP，交上周边于0.644，得此治愈率平方根的反正弦值，即sin-¹＝0.644 （弧度）。
例2 求例1中治愈率的95%可信区间。
在平方根纸上，常取实测点的三角形作图。实测点P(X,Y)的三角形是以(X,Y)、(X+1,Y)、(X,Y+1)为顶点的直角三角形。(X+1,Y) 与(X,Y+1)两顶点与分割线的垂直距离中较长者称为长距离，较短者称为短距离。先作实测点(62,110)的三角形； 再从α尺上量出uα/2的长度，此例应取u0.025；以u₀.₀₂5为半径，以三角形斜边两顶点为圆心，分别向上、向下划半圆（半圆及其圆心在分割线同一侧）; 然后从原点分别向两个半圆作切线，交四分圆于L和U，此两点的横坐标即所求95%可信区间的下限和上限，故区间为29～43%。
例3 例1中用甲疗法治某病患者的同时，又用乙疗法治相同条件患者155例，治愈100例，问乙疗法是否优于甲疗法？
H₀:π₁＝π₂ =π （合并治愈率）,
H₁: π₁<π₂。单侧α=0.05。
治愈率： 甲疗法p₁＝62/172=0.360,
乙疗法p₂＝100/155=0.645;

先按分割比(62+100):(172+155-62-100)作分割线；再分别作实测点(62,110)和(100,55)的三角形，并分别求出两三角形离分割线的短距离d₁和d₂；然后将d₁+d₂的长度与σ尺比较，由下列界值得P，按所取检验水准作出推断结论：

P	0.05	0.01
双侧检验	2.77σ	3.64σ
单侧检验	2.33σ	3.29σ

本例单侧检验，(d₁+d₂)>4σ，故P<0.01，因此按α=0.05水准拒绝H₀，接受H₁，可认为乙疗法优于甲疗法。
例4 观察某药的预防效果，服药组1966人中发病6人，发病率3.1‰；对照组445人中发病6人，发病率13.5‰；问服药组发病率是否低于对照组？
H₀:π₁＝π₂
H1:π₁<π₂。
单侧α=0.05。
先求X=0.0031×445=1.38，在横轴上点出1.38和对照组的发病人数6；量出两点间距离，再从σ尺上量出同等距离，在α尺上相应的读数即为P值，本例P<0.01; 按单侧α=0.05水准拒绝H₀，接受H₁，故可认为服药组发病率低于对照组。
例5 设某实验需用白兔200只，根据过去经验，白兔中不合该实验条件的占4%。为取得200只符合实验条件的白兔，计划用量应订为多少(取α= 0.05)?
先按分割比4:(100-4)划分割线，在分割线右侧划一条距离为U0.05的平行线；再在纵坐标为200+1处划平行于横轴的直线，交所作平行线于M；然后读出M点的横坐标为14.2，取进位的整数15；即计划量订为200+15=215只时，才有95%的可能取得200只符合实验条件的白兔。