希尔伯特公理体系xierbote gongli tixi

一种公理化的形式几何系统.在希尔伯特公理体系里，有三个基本元素：点、直线、平面；有三个基本关系：结合关系、顺序关系、合同关系.这六个基本概念满足下面的公理：
公理Ⅰ 结合公理（从属公理或关联公理）
Ⅰ₁对于任意两个不同的点A,B，存在着直线a通过A点及B点.
Ⅰ₂对于任意两个不同的点A,B，至多存在着一条直线通过A点及B点.
Ⅰ₃在每条直线上至少有两个点；至少存在着三个点不在一条直线上.
Ⅰ₄对于不在一条直线上的任意三个点A,B,C，存在着平面a通过每个点A,B,C.在每个平面上至少有一个点.
Ⅰ₅对于不在一条直线上的任意三个点A,B,C，至多有一个平面通过每个点A,B,C.
Ⅰ₆若直线a上的两个点A,B在平面a上，则直线a上任何一点都在平面a上.
Ⅰ₇若两个平面有一个公共点，则它们至少还有第二个公共点.
Ⅰ₈至少存在四个点不在一个平面上.
公理Ⅱ 顺序公理
Ⅱ₁若点B在点A和点C之间，则A,B,C是一条直线上的不同三点，且B也在C,A之间.
Ⅱ₂对于任意两点A和B，直线AB上至少有一点C，使得C在A,B之间.
Ⅱ₃在一条直线上的任意三点中，至多有一点在其余两点之间.
Ⅱ₄ 巴士公理 设A,B,C是不在一条直线上的三个点，直线a在平面ABC上但不过A,B,C中任一点.若a过线段AB的一个内点(希尔伯特定义线段AB为两个不同点A,B的集合；A,B叫做端点；A,B之间的点叫做线段AB的内点)，则a也必过线段AC或BC的一个内点.
公理Ⅲ 合同公理(‘合同’记作‘≡’)
Ⅲ₁若A,B是直线a上两点，A′是直线a或另一条直线a′上的一点，则在a或a′上点A′的某一侧必有且只有一点B′，使得A′B′≡AB.又AB≡BA.
Ⅲ₂若两线段都合同于第三线段，则这两线段也合同.
Ⅲ₃设AB,BC是直线a上的两线段且无公共内点，A′B′,B′C′是a或另一直线a′上的两线段也无公共内点.若AB≡A′B′,BC≡B′C′，则AC≡A′C′.
Ⅲ₄设平面a上给定一角∠(h,k)，在a上或另一平面a′上给定直线a′和a′所确定的某一侧.若h′是a′上以点O′为端点的射线，则必有且只有一条以O′为端点的射线k′存在，使得∠(h′,k′)≡∠(h,k). 又∠(h,k)≡∠(k,h).
Ⅲ₅设A,B,C是不在一条直线上的三点，A′,B′,C′也是不在一条直线上的三点.若AB≡A′B′,AC≡A′C′,∠BAC≡∠B′A′C′，则∠ABC≡∠A′B′C′,∠ACB≡∠A′C′B′.
公理Ⅳ 平行公理
过定直线外一点，至多有一条直线与该直线平行.
公理V 连续公理
V₁ 阿基米德公理 若AB和CD是任意两线段，则以A为端点的射线AB上必有如此的有限个点A₁,A₂，…，A_n，使得线段AA₁,A₁A₂，…，A_n-1A_n都和线段CD合同，而且B在A_n-1和A_n之间.
V₂一直线上的点集在保持公理Ⅰ₁,Ⅰ₂,Ⅱ,Ⅲ₁,Ⅴ₁的条件下，不可能再行扩充.
上述三个基本元素、三个基本关系和五组公理（共二十条）组成了希尔伯特公理体系，列表如下：

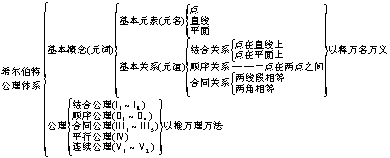
这个公理体系组成了平面几何及立体几何的完整的公理系统.它建立了一种用公理系统定义几何的基本对象及其关系的研究方法，这就是数学中的公理法.