工具变量法Instrumental Variable Method

用工具变量替换模型中不能满足假定条件的解释变量进而改善模型参数估计量特性的一种估计方法。工具变量法的关键是选择一个有效的工具变量。由于工具变量选择中的困难，工具变量法本身存在两方面不足：一是由于工具变量不是唯一的，因而工具变量估计量有一定的任意性；二是由于误差项实际上是不可观测的，因而要寻找严格意义上与误差项无关而与所替代的随机解释变量高度相关的变量事实上是困难的。

工具变量法instrumental variables

对于回归方程

y_1i＝β₁x_1i+…+β_kx_ki+u_i

i=1，…，n (1)

其中解释变量的一部分是随机的，另一部分是确定性的。由于随机的解释变量与随机干扰项相关，致使OLS法得到的参数估计不是一致估计。工具变量法是在这种情况下得到参数一致估计的常用方法。希望能找到一些变量来替代方程右端中的随机解释变量，这些变量具有下列性质：
❶必须是外生变量，与结构方程中的随机扰动项不相关；
❷必须与将要替代的方程中的随机解释变量高度相关；
❸必须与已经出现在结构方程中作为解释变量的外生变量相关性极小以避免多重共线性；
❹引入的多个替代变量之间的相关性必须极小，以避免多重共线性。用这些变量去替代方程右端的随机解释变量，方程将满足OLS的应用假设条件。这些变量起了“工具”的作用，故名“工具变量法”。
将(1)表示为：

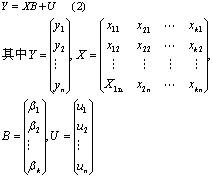
因为解释变量中有随机变量，可应用工具变量法，选择工具变量Z代替X，用工具变量乘方程(2)两边：

Z′Y=Z′XB+Z′U

由于工具变量与随机干扰项不相关，因而Z′U为0，就得到工具变量法的参数估计

Z′Y=Z′XB

＝(Z′X)^-1Z′Y

(3)