层次分析法

见“直接成分分析法”。

层次分析法

也称“层次分析”“直接组成成分分析法”“直接成分分析法”“IC分析方法”。语法结构分析方法之一； 多用于句法分析。这种方法对语法结构逐层二分 （遇到并列结构时采取多分），顺次找出结构的直接组成成分，通常分析到不能再切分为止，也可以视需要和目的而定。对结构ABCDEFGH先切分成ABCD和EFGH，然后将ABCD切分成AB和CD，将EFGH切分成EF和GH; 再将AB切分成A和B，将CD切分成C和D，将EF切分成E和F，将GH切分成G和H。例如 “我哥哥的老师的书”，首先分成 “我哥哥的老师的”和 “书”两个成分，然后再对前一部分进行类似的分析。又如“一件新的白色短袖衬衫”，首先切分成 “一件”和“新的白色短袖衬衫”两个成分，然后再切分成 “新的” 和“白色短袖衬衫”两个成分，等等。再如 “很有几分意见”，第一层切在 “很” 之后，第二层切在 “有”之后，第三层切在 “几分”之后。层次分析与 “直接 （组成）成分”“向心结构”“离心结构”等概念密切相关，这后几个术语都是美国描写语言学派提出来的。三、四十年代，层次分析的有关内容开始引入汉语语法学界，50年代、60年代，中国科学院语言研究所语法小组 《语法讲话》、高名凯《语法理论》、饶继庭 《很+动词结构》、张志公《语法学习讲话》、朱德熙《论句法结构》等等论著对层次分析方法及相关的学说进行了较详细的介绍和应用。70年代后期以来，层次分析（法）在汉语语法学中得到了普遍的重视和广泛的运用。层次分析法的实质在于找出语法结构（语言片断）的直接组成成分，将结构中的各种语法成分切分、显示出来，从而展示语言结构本来有的层次。通常这种方法的运用，人们可正确地认识语言结构的层次性，从而正确地分析语法结构，避免用词造句上的某些错误。汉语语法学者在学习和运用层次分析法的过程中，充分注意到了汉语的特点，改变了早期美国描写语言学派通常只讲结构层次而不重结构关系的做法，在对语法结构进行层次解剖的同时，加强了对直接成分之间的结构关系的说明和解释，从而充实了层次分析法的内容。参见“直接成分” “二分法” “向心结构”。

078 层次分析法

分析句法结构的方法。又叫直接成分分析法或两分法。这种析句法在分析句法结构(词组或句子)时，采取逐层剖分的方法，顺次找出每一构造层次的直接组成成分，一直分析到词为止。例如：

这个图式反映了层次分析法不是一下子把0直接分成3、4、5、7、9、10等六个词，而是先把0分成1和2两部分，然后又把1分成3和4两部分，把2分成5和6两部分，6又可以分成7和8两部分，这样分析下去，一直到词为止。例中的1和2叫做0的直接成分，3和4叫作1的直接成分。这种顺次找出一个语言片断的直接成分的手续叫作层次分析。大部分句法结构都是由两个直接成分组成的，因此层次分析一般总是采用二分的方法。层次分析法的优点是能清晰地揭示句法结构的内在构造层次。它还能分化和解释某些句法结构因可能有不同构造层次而产生的歧义现象。例如：

如上图式所示，这个句子的主语部分有两种可能的构造层次。第1种层次是指“两个汽车运输班”的司机参加了抢险工作，具体司机人数不明。第2种构造层次是指只有“两个”司机参加了抢险工作。层次分析能分化出这类句子的歧义，句子成分分析法则做不到这一点。

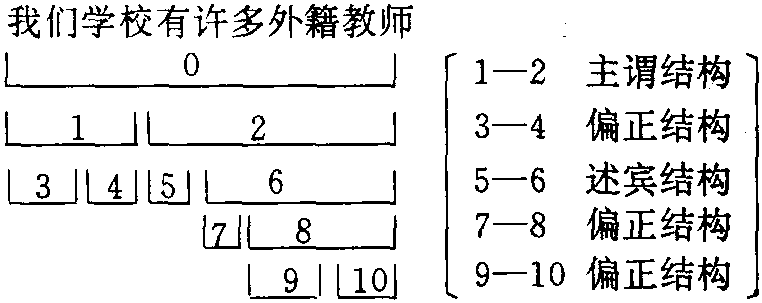
层次分析法

又称“直接成分分析法”、“二分法”。语法分析方法之一。分析一个语言片断时，采取一分为二，逐层剖析的方法来划分其结构。即先把整个片断分为两部分，然后把分出的部分再各分为两部分，这样不断二分，一直分到词为止。

层次分析法

简称“AHP方法”。定性分析与定量分析相结合的分层次进行的多目标决策方法。由美国萨蒂教授于20世纪70年代提出。

层次分析法The Analytic HierachyProcess

简称AHP法，一种实用的多准则决策方法，运筹学中的一个新分支。它能把一个复杂问题表示为有序的递阶层次结构，通过人们的判断，对决策方案的优劣进行排序，供决策参考。这一方法能够统一处理决策中定量与定性因素，具有实用性、系统性、简洁性等优点，特别适合在社会经济系统的决策分析中使用。运用AHP法解决问题，大体可分为四个步骤： (1) 建立问题的递阶层次结构。把复杂的问题分解为若干部分 （或称要素），将这些要素按属性分为若干组，形成不同层次。一般有表示分析问题目的的目标层、表示实现目标评价标准的准则层 （可分为若干子层次） 及表示实现目标备选方案的方案层（见下图）。同一层次的要素作为准则，对下一层次的某些要素起支配作用，同时又受上一层次要素的支配。(2) 构造两两比较判断矩阵。AHP递阶层次结构形成后，上下层次之间要素的隶属关系就被确定下来。假定上一层次的要素Ck作为准则，对下一层次要素A_1,A₂…A_n有支配关系 （即结构图中有连线的），则取如下形式构造比较判断矩阵：

Ck	A1	A2	…	An
A1 A2 … An	a11 a21 … an1	a12 a22 … an2	… … …	a1n a2n … ann

矩阵中元素a_ij的值为同层次各要素对上一层次某一准则的比较判断值，根据人的判断能力按下表中1—9的标度取值。(3) 层次单排序，计算单一准则下要素的相对重要权值。通过计算比较判断矩阵A的最大特征根λmax与特征向量，以其规一化的特征向量W=(w1、w2…wn)值作为同一层次n个要素A1、A2…A_n对上一层次某一准则C_k的相对重要性排序权值。W是否能作为排序权重使用，还需通过对比较判断矩阵的一致性检验，检验可依如下程序进行：
❶计算一致性指标;
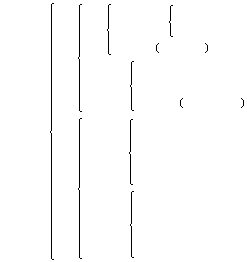❷计算平均随机一致性指标R.I.，可查下表：

阶数n	1	2	3	4	5	6	7	8	9	10	11	12
R.I	0	0	0.52	0.89	1.12	1.26	1.36	1.41	1.46	1.49	1.52	1.54

❸计算一致性比率C.R,C.R=C.I/R.I，当C.R<0.1时，认为判断矩阵的一致性是可接受的，否则要重新构造比较判断矩阵。(4)层次总排序，计算层次结构中每一层次中所有要素相对于总目标 （最高层） 的相对组合重要性权值。若已经计算出第k-1层元素相对于总目标的排序权值向量αk-1=(αk-1/1,αk-1/2…αk-1/m)，第k层在第k-1层以第j个元素为准则下的排序向量为bkj=(bk1j、bk2j…bknj)，矩阵Bk=(bk1、bk2…bkn)。则第k层n个要素相对于总目标的组合排序权值为αk=Bkα^k-¹。这种计算可根据递阶层次结构从上至下逐层计算，直至求出最下层（各种方案）对最高层（总目标）的重要性排序权值，作为进行决策的依据。同样，对于总排序值亦要作出相应的一致性检验。AHP法由美国匹兹堡大学运筹学教授A.L.Saaty在70年代提出，在1982年北京举行的“中美能源、资源、环境”会议期间介绍到我国。我国学者近几年将它应用于能源规划、资源分配、人口研究、企业生产经营、科研成果评价、干部评价等问题上都取得了成果。AHP法以其理论充分、形式简单、灵活方便，在社会经济系统的分析中，越来越得到人们的普遍重视。

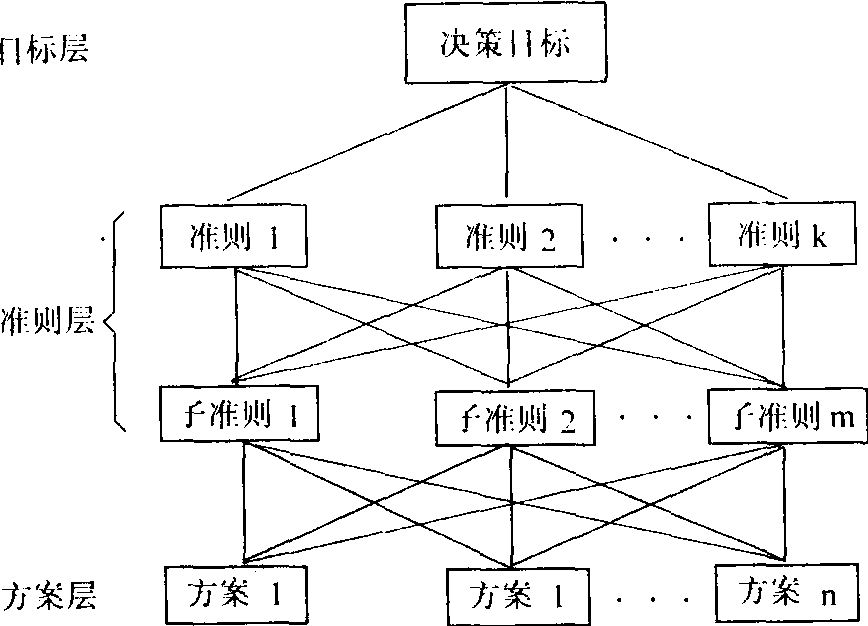
AHP层次结构图

判断矩阵标度及其含义

标度	含 义
1 3 5 7 9	表示两个要素相比，具有同样重要性 表示两个要素相比，一个要素比另一个要素稍微重要 表示两个要素相比，一个要素比另一个要素明显重要 表示两个要素相比，一个要素比另一个要素强烈重要 表示两个要素相比，一个要素比另一个要素极端重要

注：
❶2、4、6、8可作为上述相邻判断的插值；
❷若要素i与j比较得aij，则要素j与i比较判断值为1/aij