射影几何

几何学的一门分科。一图形经过有限次透视后变成另一图形时，称射影对应。射影几何研究的就是经过射影对应后图形的不变性质。所谓透视，在平面上（空间中）把直线（平面）的点，经过中心投影（包括平行投影）投到另一平面上。在测量、航空等方面应用较广。

射影几何

是一种专门用来讨论在把点射影到直线或平面上时，图形不变的性质的几何。欧氏几何是射影几何的子几何。首先系统地研究射影几何的是法国陆军军官J.V.邦瑟勒(1788—1867),1812年他著述了《论图形的投影几何性质》一书。射影几何的特性是：在它所论及的两组图象(如两条直线上的点，两束直线，这里每一直线束是由过一点的所有直线组成)之间确定了一个保持交比的一一对应。比如，设pi,pi′1788—1867,1812年他著述了《论图形的投影几何性质》一书。射影几何的特性是：在它所论及的两组图象(如两条直线上的点，两束直线，这里每一直线束是由过一点的所有直线组成)之间确定了一个保持交比的一一对应。比如，设pi,pi′(i=1,2,3,4)是两条直线上对应的点，xi,xi′(i=1,2,3,4)是它们相对应的坐标，则关系式：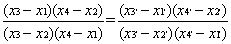

成立。一维形式之间的一切这种对应关系都可由线性变换x′=ax+b/(cx+d)(ad-bc≠0)给出；二维形式之间的这种对应关系则由行列式|aij|(i,j=1,2,3,4)不为零的关系式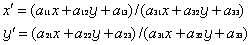

给出，它构成了一个八参数的群，即平面上的射影群。