导数
导数daoshu
是微分学的基本概念之一。设函数y=f (x)在点x0的某个邻域内有定义,当自变量x在x0处有改变量Δx时,函数相应的改变量为Δy=f (x0+Δx) -f (x0)。若极限
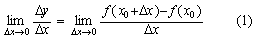
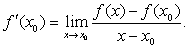
若函数f (x)在开区间(a,b)内的每一点都可导,则称函数f (x) 在开区间 (a,b) 内可导。
若函数f (X)在开区间 (n,b) 内可导,则f (x)在点x0处的导数由x0唯一确定,所以f (x)的导数仍是x的函数,称为f (x) 的导函数,记作f′ (x)。
函数的导数值f′ (x0)反映了函数f (x)在点x0附近变化的快慢程度。导数在实际问题中有着广泛的应用。
例如,运动的瞬时速度v (t)是路程s (t)对时间t的导数,即v (t ) =s ′ (t)。
又如,电流强度i (t)是电量Q (t)对时间t的导数,即i (t) =Q ′ (t)。
在微积分产生之初,导数概念就是从不同角度引出的。牛顿从研究运动的瞬时速度问题入手,引出导数概念(1687年),莱布尼兹则是由研究曲线的切线问题而引出导数概念的 (1684年)。
☚ 变化率 导数的几何意义 ☛
导数
又称“微商”。设一元函数y=f(x),当自变量从x变化到x+△x,函数值从f(x)变化到f(x+△x)时,函数值的增量与自变量增量比值的极限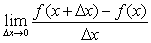 若是存在,则称此极限为f(x)在x的导数。记为f′(x)或dy/dx。研究多元函数导数时,考虑函数对某一变元的变化率。例如设二元函数f(x,y),如果x的变增量为△x,函数值有增量f(x+△x,y)-f(x,y);当此增量与△x的比值极限存在,就称函数对x的偏导数存在。记作
若是存在,则称此极限为f(x)在x的导数。记为f′(x)或dy/dx。研究多元函数导数时,考虑函数对某一变元的变化率。例如设二元函数f(x,y),如果x的变增量为△x,函数值有增量f(x+△x,y)-f(x,y);当此增量与△x的比值极限存在,就称函数对x的偏导数存在。记作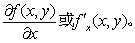
- 说文解字义证是什么意思
- 说文解字五音韵谱是什么意思
- 说文解字今释是什么意思
- 说文解字六书疏证是什么意思
- 说文解字叙是什么意思
- 说文解字古今音读是什么意思
- 说文解字句读是什么意思
- 说文解字引方言考是什么意思
- 说文解字引经考是什么意思
- 说文解字引群书考是什么意思
- 说文解字引论是什么意思
- 说文解字引通人说考是什么意思
- 说文解字斠诠是什么意思
- 说文解字旧音是什么意思
- 说文解字校勘记残稿是什么意思
- 说文解字校录是什么意思
- 说文解字段注考正是什么意思
- 说文解字注是什么意思
- 说文解字注匡谬是什么意思
- 说文解字注笺是什么意思
- 说文解字略例是什么意思
- 说文解字研究是什么意思
- 说文解字研究法是什么意思
- 说文解字篆韵谱是什么意思
- 说文解字系传是什么意思
- 说文解字索隐是什么意思
- 说文解字约注是什么意思
- 说文解字群经正字是什么意思
- 说文解字翼征是什么意思
- 说文解字补义是什么意思
- 说文解字诂林是什么意思
- 说文解字读是什么意思
- 说文解字辨证是什么意思
- 说文解字通正是什么意思
- 说文解字通论是什么意思
- 说文解字部首校释是什么意思
- 说文解字音韵表是什么意思
- 说文解字韵隶是什么意思
- 说文订订是什么意思
- 说文论正是什么意思
- 说文诂林是什么意思
- 说文话是什么意思
- 说文说是什么意思
- 说文读若考是什么意思
- 说文谐声是什么意思
- 说文谐声孳生述是什么意思
- 说文谐声类编是什么意思
- 说文谐声谱是什么意思
- 说文辨字正俗是什么意思
- 说文辨疑是什么意思
- 说文述谊是什么意思
- 说文通检是什么意思
- 说文通训定声是什么意思
- 说文通训定声补遗是什么意思
- 说文通论是什么意思
- 说文逸字是什么意思
- 说文逸字辨证是什么意思
- 说文逸字附录是什么意思
- 说文部目便读是什么意思
- 说文部目分韵是什么意思