密度函数
全称“分布密度函数”。定义如下:若在实数域上存在非负可积函数f(x),使得随机变量ξ取值于任一区间(a,b)的概率
![]()
密度函数Denstity Function
连续型随机变量ξ落在区间|x,x+Δx|内的概率P (x<ξ ∫abf(x) dx=1 F (x) =P(-∞<ξ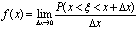
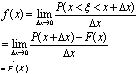
- 孙过庭书谱序是什么意思
- 孙过庭草书书谱是什么意思
- 孙过庭草书千字文是什么意思
- 孙运珍是什么意思
- 孙运球是什么意思
- 孙运璇是什么意思
- 孙运璇内阁是什么意思
- 孙远志是什么意思
- 孙连仲是什么意思
- 孙连奎是什么意思
- 孙迪是什么意思
- 孙迪方是什么意思
- 孙述万是什么意思
- 孙迴璞是什么意思
- 孙迺琨是什么意思
- 孙逊是什么意思
- 孙逊群是什么意思
- 孙逖是什么意思
- 孙逖《宿云门寺阁》 - 唐山水诗赏析是什么意思
- 孙逖集是什么意思
- 孙通是什么意思
- 孙逢吉是什么意思
- 孙逢祯是什么意思
- 孙逢铎是什么意思
- 孙逸是什么意思
- 孙逸仙是什么意思
- 孙逸仙博士代表团是什么意思
- 孙逸春晓图扇页是什么意思
- 孙遇是什么意思
- 孙道临是什么意思
- 孙道仁是什么意思
- 孙道升继妻兰氏的人物故事|评价|小传,孙道升继妻兰氏的事迹|史鉴是什么意思
- 孙道同是什么意思
- 孙道天是什么意思
- 孙道平是什么意思
- 孙道温妻赵氏的人物故事|评价|小传,孙道温妻赵氏的事迹|史鉴是什么意思
- 孙道滋是什么意思
- 孙道相是什么意思
- 孙道粹是什么意思
- 孙道绚是什么意思
- 孙道绚(《全宋词》:ⅱ1247)是什么意思
- 孙道绚《忆秦娥》是什么意思
- 孙道绚《滴滴金》是什么意思
- 孙道绚《滴滴金梅》是什么意思
- 孙道雄是什么意思
- 孙遵法是什么意思
- 孙邕是什么意思
- 孙邦是什么意思
- 孙邦佐是什么意思
- 孙邦华是什么意思
- 孙邰是什么意思
- 孙郁是什么意思
- 孙郃是什么意思
- 孙郎是什么意思
- 孙郎婿是什么意思
- 孙采珠是什么意思
- 孙采邻是什么意思
- 孙里人是什么意思
- 孙重贵是什么意思
- 孙重进是什么意思