密克定理
密克定理mike dingli
在△ABC三边BC,CA,AB所在直线上分别取X,Y,Z三点.则⊙AYZ,⊙BZX,⊙CXY三个圆共点.如图.
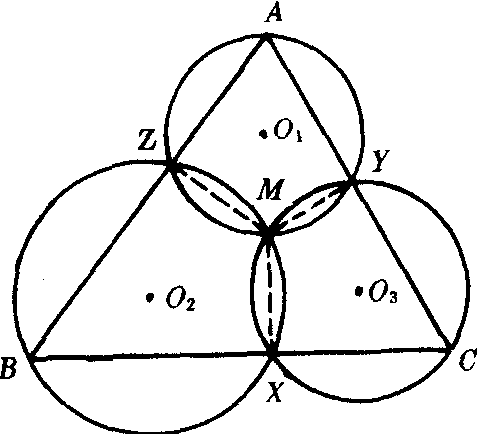
这个定理是密克于1838年叙述并予以证明的.三个圆的公共点M叫做X,Y,Z三点对于△ABC的密克点.
设⊙BZX与⊙CXY交于M点,连结MX,MY,MZ,因为B,X,M,Z四点共圆,C,X,M,Y四点共圆,所以∠AYM=∠CXM=∠BZM,故A,Y,M,Z四点共圆(四边形AYMZ的外角等于其内对角).因此⊙AYZ,⊙BZX,⊙CXY三个圆共点.
当Z于A点重合时,则过A,Y与AB相切的圆当作⊙AYZ.若Y,Z重合于A,则以A点代替⊙AYZ,此时认为点A为“点圆”,其余仿此讨论.
☚ 共点圆 三角形的九点圆 ☛
- nightingale,florence是什么意思
- nightjar是什么意思
- nightly是什么意思
- night-mare是什么意思
- nightmare是什么意思
- nightmares是什么意思
- night-rule是什么意思
- nightshade是什么意思
- night-tripping是什么意思
- nigrahasthana是什么意思
- nih是什么意思
- nihalani是什么意思
- nihalchand kishangarh是什么意思
- nihil是什么意思
- nihilism是什么意思
- ni hka是什么意思
- nihon是什么意思
- nihpot是什么意思
- niigata是什么意思
- niit(national information institute of technology)是什么意思
- nijalingappa siddavanahalli是什么意思
- ni jianl zix是什么意思
- nijmegen是什么意思
- nijmegen,treaties of是什么意思
- nijni-novgorod 下诺夫哥罗德是什么意思
- nikaya是什么意思
- nike是什么意思
- nikephoros([ˈnikifəurəs])ⅰ是什么意思
- nikharvata是什么意思
- nikisch,arthur是什么意思
- nikkei average是什么意思
- nikkei index是什么意思
- nikkei stock average是什么意思
- nikko是什么意思
- nikolas roerich是什么意思
- nikolayev是什么意思
- nikolaïev 尼古拉耶夫是什么意思
- nikopol是什么意思
- nikosha是什么意思
- niksubha是什么意思
- nikumbha ⅰ是什么意思
- nikumbha ⅱ是什么意思
- nikumbha ⅲ是什么意思
- nikumbha ⅳ是什么意思
- nikumbha ⅴ是什么意思
- nikumbha ⅵ是什么意思
- nikumbhila是什么意思
- ni kvt是什么意思
- nil是什么意思
- nila是什么意思
- nilagiri是什么意思
- nilakantha是什么意思
- nilakantha diksitar是什么意思
- nilapita是什么意思
- nila ⅰ是什么意思
- nila ⅱ是什么意思
- nila ⅲ是什么意思
- nila ⅳ是什么意思
- nila ⅴ是什么意思
- nila ⅵ是什么意思