容斥原理rongchi yuanli

设S是含有有限个元素的集合，P₁和P₂是S中的每个元素可能具有或可能不具有的两个性质.若计算S中既不具有性质P₁也不具有性质P₂的元素个数，则首先计算S的所有元素，其次从中去掉具有性质P₁的所有元素和具有性质P₂的所有元素，注意到已两次去掉那些同时具有P₁和P₂性质的元素，因此再重新计入所有这种元素一次.用符号表示如下：
设A₁是S的具有性质P₁的元素的子集合，A₂是S的具有性质P₂的元素的子集合，那么是由S的不具有性质P₁的那些元素组成，是由S的不具有性质P₂的那些元素组成，集合∩的元素既不具有性质P₁也不具有性质P2的那些元素，其元素个数为|∩|=|S|-|A₁|-|A₂|+|A₁∩A₂|.或者表示成n(∩)=n(S)-n(A₁)-n(A₂)+n(A₁∩A₂)。
一般地，令P₁,P₂，…，p_m是S中的每个元素可能具有或可能不具有的m个性质.对于i=1,2，…，m，令A_i是S的具有性质P_i（可能还有其它性质）的元素子集合，则A_i∩A_j(i≠j)是同时具有性质P_i和P_j（可能还具有其它性质）的那些元素的子集合，A_i∩A_j∩A_k(i≠j≠k)是同时具有性质P_i,P_j和P_k的那些元素的子集合，等等.不具有所有这些性质的任何一个元素的子集合是∩∩…∩。
不具有性质P₁,P₂，…，Pm的任何一个S的元素个数由下式给出

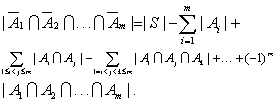
利用集合运算的性质，又可得到S的至少具有性质P₁,P₂，…，P_m中的一种性质的那些元素的个数

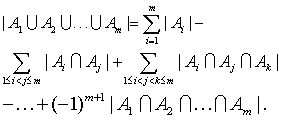
利用上述式子计算集合元素的个数，首先计算包容了的元素个数，但包容中有重复计算时，要排除掉某些重复计算的元素的个数，当排除过多时，又要包容进来，……，如此继续下去，就得到所求元素的个数.这是计数方法中的一条原理，被称为容斥原理，又称包含排斥原理.这条原理首先由J.J.西尔维斯特创立的，其后H.J.庞加莱把这条原理推广到概率论中加以应用。

容斥原理Rongchi yuanli

是组合学的基本原理之一，可以看作通常的加减法的推广，它告诉人们。在计数的时候，怎样才能做到既无遗漏，又无重复，从而保证计数结果的正确性。例如，已知某班有男生21名，女生19名，要求班里学生总数，这个问题直接用加法就可以解决，但若问：已知有10人语文考试得90分以上，有15人算术考试得90分以上，那么两门课中至少有 一门考试成绩在90分以上的同学有多少， 这个问题，直接相加就不行了，必须考虑到有多少人两门课都在90分以上，比如说有5人，那么正确的结果应当是10+15-5=20, 这是因为10+15中， 两科都超过90的5名学生被计算了两次， 我们再来看一个稍复杂一点的例子：求小于30并与30互素的自然数个数。这个问题用逐个判别的办法肯定能得到正确的结果， 小于30且与30互素的数有1、7、11、13、17、19、23、29共8个。但若把30换成更大的数， 例如2 431, 这种办法就不可取了。利用容斥原理，可以这样分析，因为30=2×3×5，与30互素意味着不是2、3或5的倍数，不大于30的自然数中有15 (=30÷2) 个数是2的倍数， 10 (=30÷3)个3的倍数， 6 (=30÷2) 个5的倍数，我们从30个数中把2、3及5的倍数排除，用减法得30-15-10-6=-1, 这当然还不是正确结果，因为2与3的公倍数(有5个数)被排除了两次，同样3与5的公倍数(有2个),5与2的公倍数(有3个)也被排除了两次，据此修改我们的算式为30-15-10-6+5+3+2=9, 这仍然不是最后结果， 因为2、3、5的公倍数30，在-15, -10, -6时被排除了三次，但在修正时(+5、+3、+3) 又被添上了三次，等于未被排除，因此最终应修改算式为30-15-10-6+5+3+2-1=8，同样道理，由于2 431=11×13×17，小于2 431且与2 431互素的数有2 431-143-187-221+17+13+11-1=1 920。
容斥原理是局部与整体之间关系的一个原理， 研究这一类问题时，人们习惯于依照事物特征进行分类，倘若分类是不完全的， 那么不同的类之间可能有公共部分，于是在考虑整体及各类的数量关系时，就需要把公共部分排除。这一原理有助于培养学生不重复、不遗漏。全面细致地分析和解决问题的能力。