套利定价理论Arbitrage Pricing Theory(APT)

美国经济学家斯蒂芬·罗斯在1976年提出的一个均衡资产定价模型。其首要的假设是，每个投资者都会去利用不增加风险的情况下能够增加组合的回报率的机会。利用这种机会的具体做法是使用套利组合。套利定价理论的基本假定是证券的回报率与未知数量的未知因素相联系。假设条件有：投资者具有相同的预期；投资者是厌恶风险者和追求最大效用者； 市场是完善的，没有交易费用等市场障碍。套利定价模型表达式为E(R_i)=R_f+λ₂b_i2+…+λ_kb_ik。其中，E(R_i)是资产i的期望收益率，b_i1到b_ik是第1种到第k种情况下资产i的单位超额收益率，R_f是无风险收益率，λ₂到λ_k是对应的风险因子。该模型表明，资本资产的收益率是各种因素综合作用的结果，如GDP增长、通货膨胀水平等因素也会产生影响，而不是仅仅受证券组合内部风险因素的影响。

套利定价理论arbitrage pricing theory,APT

套利定价理论是一个均衡资产定价模型，其首要的假设是，每个投资者都会去利用不增加风险的情况下能够增加组合的回报率的机会。利用这种机会的具体做法是使用套利组合。套利定价理论的出发点是假设证券的回报率与未知数量的未知因素相联系。在只有一个因素时，证券的回报率联系着如下的单因素模型：

r_i＝a_i+b_iF₁+e_i (1)

其中：r_i——证券i的回报率；
F₁——因素值；
b_i——证券i对因素的敏感性；
e_i——随机误差。
假设投资者持有等金额的n种证券，根据套利定价理论，投资者将竭力发现构造一个套利组合的可能性，以便在不增加风险的情况下，增加组合的预期回报率。首先，套利组合不需要投资者任何额外资金，如果X_i表示投资者对证券i的持有量的变化，这一要求可以表述为：

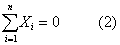
其次，一个套利组合对任何因素都没有敏感性，这一性质可表述为：

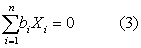
两个方程和n(n≥3)个未知数，表明无限多组满足方程(2)和(3)的X₁、X₂…X_n。当这个套利组合满足第三个要求：

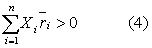
其中_i代表i种证券的预期回报率时，这样一个套利组合对任何一个渴望高收益且不关心非因素风险的投资者是具有吸引力的，它不需要任何额外的资金，没有任何因素风险，却能带来正的预期回报率。
于是每个投资者都将根据这样的套利组合买入卖出某种证券，这种买卖行为持续到所有套利机会明显减少或消失为止。此时，预期回报率与敏感性将近似满足如下的线性关系：

_i＝λ₀+λ₁b_i (5)

其中λ₀和λ₁为常数。当回报率是由一个因素产生时，这个方程就是套利定价理论的资产定价方程。如图，分别以i种证券的预期回报率_i和因素敏感性b_i为纵坐标和横坐标，画出套利定价理论的资产定价线。对于一个因素敏感性和预期回报率都没有落在资产定价线上的证券，其定价就是不合理的，如图中证券B。投资者将以相同金额分别买进证券B和卖出证券S，就构成了一个套利组合，作为购买证券B的结果，证券B的价格将上升，进而其预期回报率将下降直到它位于套利定价理论资产定价线上为止。
套利定价理论中定价方程的第二种形式是：

_i＝r_f+(δ₁-r_f)b_i (6)

其中：r_f——无风险资产的预期回报率；
δ₁——对因素有单位敏感性的组合的预期回报率。
在k个因素(F₁,F₂…F_k)的情形下，每一个证券都将具有k个敏感性(b_i1,b_i2，…b_ik)。定价方程可以表示为：

_i＝λ₀+λ₁b_i1+λ₂b_i2+…+λ_kb_ik (7)

或者：

_i＝r_f+(δ₁-r_f)b_i1+(δ₂-r_f)b_i2+…+(δ_k-r_f)b_ik (8)

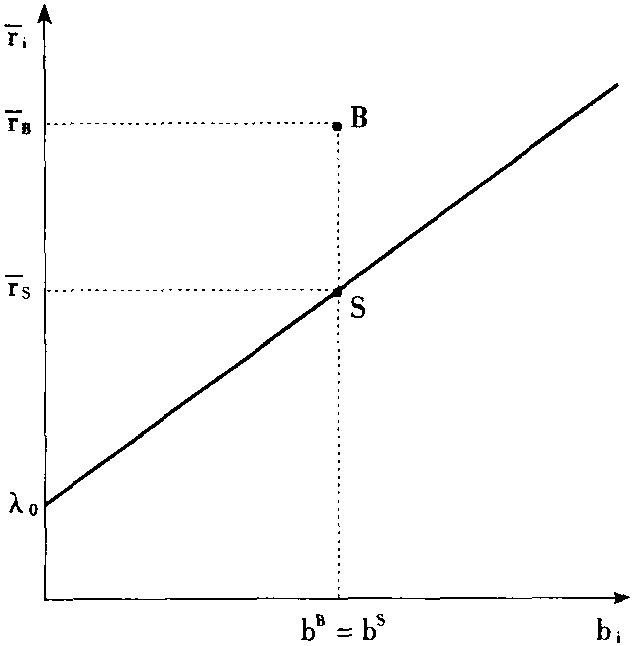
套利定价理论资产定价线