一次指数平滑法

---

一种常用的预测方法，是移动平均数方法的改型。

它既具备移动平均数方法的长处，又可以减少数据的存储量。包括离散时间系列指数平滑法和连续时间系列指数平滑法。

设Z₀，Z₁，…，Z_n为离散时间系列的观测值或给定数值，各观测值相对应的时间依次为t=0，1，…n；又设S₁，S₂，…S_n依次为时间t=1，2，…n时各观测值的修匀值(或称平滑值)。则各个修匀值S_t是利用下式求得：

S_t=Z_t－1+α(Z_t－Z_t－1)，t=1，2，…，n

其中S_t称为指数平滑平均数；α是一个介于0与1之间的常数，称为平滑常数。

把上式改写为：

S_t=αZ_t+(1－α)Z_t－1，t=1，2，…，n

则可看出，S_t是Z_t和Z_t－1的加权平均数，其权数分别为α与(1－α)。如果进行递推，可得

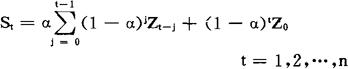
指数平滑法实际上是一种特殊的加权平均法。

由于这种特殊权数均呈j的指数函数形式，且此平均法具有修匀或平滑一系列观测值或给定数列之功能，故得指数平滑法之名称。

如果给定的时间系列Z_(t)是由连续观测值或连续数值构成，则可令t为一系列离散时间值，代入Z(t)中，求得一系列离散观测值后，再用上述离散时间系列指数平滑公式来计算。也可采用下列处理办法：

仿照离散指数平滑法的定义，得时间为t的指数平滑平均数Y(t)为

Y(t)=αZ(t)+(1－α)Y(t－1)

t=1，2，…，n，0＜α＜1

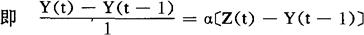
令t的相邻两数值之间隔为△t，则上式变为

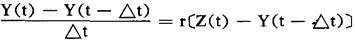
式中r为平滑常数，主动作用类似α，但它的允许变化范围并不在0与1之间，而是在0＜γ＜∞之间。

令△t→0，则上式变为

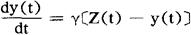
对上式进行积分，且时间t=T时，0的连续指数平滑平均数为

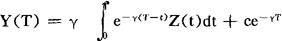
式中，C为积分常数。