一次函数的性质

---

在一次函数y=kx+b(k≠0)中：

1．当k>0时，y的值随x的增大而增大，这时函数图象从左至右上升．

2．当k<0时，y的值随x的增大而减小，这时函数图象从左至右下降．

3．k，b决定直线位置，反过来，直线的位置可决定k，b的符号．

注意 直线y=kx+b的位置与k，b的关系：

1．当k>0，b>0时，直线过第一、二、三象限(不过第四象限)．

2．当k>0，b<0时，直线过第一、三、四象限(不过第二象限)．

3．当k<0，b>0时，直线过第一、二、四象限(不过第三象限)．

4．当k<0，b<0时，直线过第二、三、四象限(不过第一象限)．

如图所示：

答 D．

[解析] 因为常数项b=－2，与y轴交点坐标为(0，－2)在x轴下方，排除A，C．

又因为y随x的增大而减小．图象从左到右下降，排除B，故选D．

例7 若一次函数y=(2－m)x+m的图象经过第一、二、四象限，则m的取值范围是＿＿．

答 m>2．

[解析] 解这类题，先画草图，根据函数图象过第一、二、四象限，说明图象从左至右下降，k<0，与y轴交点在x轴上方，b>0，故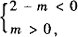∴m>2．

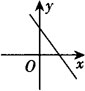
例8 直线y₁=kx+b过第一、二、四象限，则直线y₂=bx+k不经过第＿＿象限．

答 二．

[解析] 直线过第一、二、四象限，从图象中可知k<0，b>0，则新的直线y₂=bx+k中：

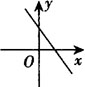
自变量的系数为b>0，说明y随x的增大而增大，图象从左至右上升，常数项为k<0，说明与y轴交点在x轴下方，故过第一、三、四象限，不过第二象限．