大数表示法Dashu biaoshifa

1637年，笛卡尔给出了正整指数幂的现代表示法。在此之前，十进位值制的印度-阿拉伯数码在欧洲已经传播了几百年。因此，从那时起，人们已经可以方便地写出任何数量级的大数。而在此之前，除了两个辉煌的特例之外，其他各古代民族和国家在这方面的能力都是相当有限的。
埃及古代使用的是非位值制的十进制，他们对1、10、100、…， 107都给出了单独的符号； 一般的数是用这些符号累积而成(参见“埃及古代数学”)。早在公元前3100年左右，他们已经可以表示以百万和十万计的大数，但此后的2000多年中，他们的大数表示法并无实质上的进步，如果不借助其他辅助手段，用他们的8个数字符号所能表示的最大数是99999999，即10⁸-1, 这需要把那8个符号每一个都连写9次。
希腊人发明过两种记数符号 (参见 “希腊古代数学”)，较流行的爱奥尼亚记数法把27个字母分为3组用以记数： 第一组表示1—9, 第 二组10—90, 第三组100——900，然后在表示1—9的字母左下角加上一撇(′), 表示1 000—9 000, 再把这4组数字符号分别写在一个表示“万”的大写字母M 上， 由相乘关系再得到4组数字符号，与古埃及的情况相同，用希腊人的这8组72个数字符号可以直接表示的最大数也是10⁸—1。
使用位值制记数法(巴比伦、中国、玛雅、印度)可以直接表示的大数当然比非位值制大得多， 但是如果不对基底的幂次采取适当的处理办法， 而仅凭数位的增加， 它能够有效地加以表示的数量级也会受到明显的局限。实际上，一个100位的大数已经足够使绝大多数现代人眼花缭乱， 更不用说再用这样的大数进行各种运算，而古人在这方面的能力显然还要低一些。当然，对古代的实际需要来说，使用十进、二十进或六十进位值制记数法，10位数左右的大数也就够了，在巴比伦和玛雅人使用的数字中从未有超出这个范围的，在中国古代，殷墟甲骨文中已经有了“三万”这样的大数。万以上的大数数名， 至迟到春秋时代 (公元前770—前476)已经出现，分十进与万进两种进位方法，常用的有亿、兆、经、姟四级，以万进方法而论，可以表示10²¹以内的一切自然数(因为一姟=10²⁰，后世又把姟写作垓)。
从现有资料看， 在古代只有希腊人和中国人对大数表示法进行过真正深入的研究。
在古希腊，公元前3世纪，阿基米德和阿波罗尼奥斯(Apollonius)分别建立了自己的大数系统，阿波罗尼奥斯的系统是一进万进制， 他称1——10⁴—1为第一级， 10⁴——10⁸—1为第二级， 10⁸——10¹²—1为第三级，依次类推。他仍使用爱奥尼亚记数符号中的前4组，记数时循环使用，并对其所在的级加以标明，于是形成了4个数字一级、每级对应于10 000的一个幂次，颇与位值制记数法相类似，后来又有不少希腊、罗马数学家对这种记数法的具体表示作过改进。阿基米德的大数系统更为庞大。由于用爱奥尼亚记数系统可以直接表示的最大数为10⁸—1, 他即以10⁸作为大数系统的基底，他称1——10⁸—1为等一级，10⁸——10¹⁶—1为第二级，10¹⁶——10^24—1为第三级， ……，在第n级中，以(10⁸)^n-1为单位。第10⁸级由(10⁸)^(108-1)——(10⁸)¹⁰8—1的所有数组成， 每一级中也可以包括前一级中的最末一数。从1到108·108—1的所有数组成了第一个 “周期”， 可以用我们的记法表示为P=(10⁸)¹⁰⁸，于是，第一个周期包括1——P—1中的所有数(也可以包括P本身)。然后，把P作为第二个周期的单位，第二周期包括P——P²—1中的所有数。……。第10⁸周期的第一级由下面的数组成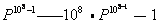
然后再逐级扩展， 直到第10⁸周期的第10⁸级， 以10⁸·¹08·P^108-1即P¹⁰⁸为最后一数， 这最后一数被阿基米德称为“第万万周期的第万万级的万万单位”，它的值是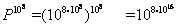
用今天的数码写出来是1后面再加上8·1016个0。这样一个庞大的大数系统在古代自然毫无用武之地， 但其中体现出来的纯粹数学思维的美却足以使后人为之倾倒。
在中国古代，南北朝北周(557——581)时甄鸾曾经注解过一本董泉撰写的《三等数》，在唐初曾作为国子监算学馆的辅助教材， 书已失传， 但在甄鸾注解的《数术记遗》(参见“《算经十书》”)中有一段简略的记载， 原文如下： “黄帝为法，数有十等。及其用也， 乃有三焉。十等者， 亿、兆、京、垓、秭、壤、沟、涧、正、载。三等者，谓上、中、下也。其下数者，十、十变之，若言十万曰亿，十亿曰兆，十兆曰京也。中数者，万、万变之， 若言万万曰亿， 万 (原文此下又衍一“万”字)亿曰兆， 万 （原文衍一万字）兆曰京也。上数者，数穷则变，若言万万日亿，亿亿曰兆，兆兆曰京也。”根据“上数”的“数穷则变”原则， 由亿开始的10个数量级的数值分别是
10⁸,10¹⁶,10³²,10⁶⁴,10¹²⁸,10²⁵⁶,10⁵¹²,10¹⁰²⁴
10²⁰⁴⁸, 10⁴⁰⁹⁶
利用这10个数量级与万以下各数的表示法，这个系统可以表示1——104 097—1之间的所有数。比之阿基米德的大数系统，这里的系统显然是小了一些，但其简捷灵便却又超过了阿基米德的系统， 这里所体现出来的纯粹数学思维的优美比之阿基米德也是毫不逊色的。实际上，这两个大数系统显然不是为了实用的目的，而是为着数学自身的完美发展起来的。