大数定律law of great numbers

又称大数法则或平均数法则。表述随机现象的大量重复中出现一定规律性的若干定律的总称。其狭义的理解是指概率论中用来阐明大量随机现象平均结果的稳定性的一系列定理。表明了必然性与偶然性之间辩证联系的规律。如进行抽样估计时，随机地从总体中抽取样本，只要样本容量充分大，样本平均数就以很大的概率接近于总体平均数。常见的大数定律表示形式为：

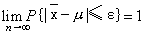
式中为样本平均数；μ为总体平均数；ε为任意小的正数；n为样本容量；P为概率。大数定律有车贝雪夫大数定律、贝努里大数定律、普阿松大数定律、辛钦大数定律、马尔科夫大数定律等。

大数定律dashu dilu

在概率论中，关于大量随机现象之平均结果稳定性的定理，阐述在何种条件下，随机事件的概率接近于0或1，即在何种条件下，随机事件可以转化为不可能事件的一系列定理，这一组定理统称为大数定律，常见的大数定律有以下几个：
契比雪夫大数定理 设随机变量X_k (k=1,2，…)相互独立，且有相同的有限的数学期望和方差E(X_k ) =μ,D (X_k) =σ² (k=1,2，…)，则对任意的ε>0，有

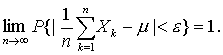
定理表明，当n很大时，随机变量X₁,X₂，…，X_n的算术平均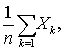接近于数学期望E (X₁ ) =E(X₂ )=…=E (X_n) =μ，这种接近是概率意义下的接近。
贝努利大数定理 设n_A是n次试验中，事件A发生的次数，p是事件A在每次试验中发生的概率，则对于任意正数ε有

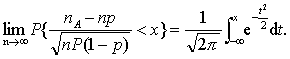
该定理表明事件发生的频率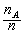依概率收敛于事件的概率P，换言之，当n很大时，事件发生的频率与概率有较大偏差的可能性很小。

大数定律

又称“平均数法则”。概率论中基本定律之一。在大量重复的随机现象中往往出现必然的结果，即样本平均数以很大的概率接近总体平均值。大数定律即这一类规律的总称。

大数定律Law of Large Number

亦称“大数法则”。描述大量随机现象之间平均结果稳定性的一系列数学定律的总称。从理论上阐述了在一定条件下，大量重复进行的随机事件的规律性和稳定性。常用的大数定律有伯努利大数定律、辛钦大数定律、柯尔莫哥洛夫强大数定律和重对数定律。

大数定律

亦称“大数法则”。描述大量随机现象之平均结果的稳定性的一系列数学定理的总称。最早的大数定律由瑞士人Jacob Bernouli1713年所发现。它以明确的数学等式表达了一种规律性，即，无论随机事件的个别结果如何不同，大量随机事件的平均结果实际上与它们没有任何关系。大数定律从理论上阐述了在一定条件下，大量重复进行的随机事件的规律性和稳定性。
具体说，大数定律描述了n个具有独立同分布的随机变量x₁x₂ …，xⁿ之和S_n当n→∞时的变化规律。这里：

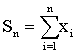
常见的大数定律有贝努利大数定律、切贝雪夫大数定律、辛钦大数定律和柯尔莫戈洛夫大数定律。
大数定律根据收敛的条件分为强大数定律和弱大数定律。前者指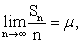即，当→∞时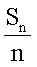，绝对收敛于μ; 后者指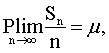当→∞时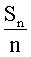，依概率收敛于μ。

大数定律Law of Large Number

亦称“大数法则”。描述大量随机现象之平均结果的稳定性的一系列数学定理的总称。最早的大数定律由瑞士人Jacob Bernouli1713年所发现。它以明确的数学等式表达了一种规律性，即，无论随机事件的个别结果如何不同，大量随机事件的平均结果实际上与它们没有任何关系。大数定律从理论上阐述了在一定条件下，大量重复进行的随机事件的规律性和稳定性。
具体说，大数定律描述了n个具有独立同分布的随机变量x₁,x₂，…，x_n之和S_n，当n→∞时的变化规律。这里：

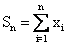
常见的大数定律有贝努利大数定律、切贝雪夫大数定律、辛钦大数定律和柯尔莫戈洛夫大数定律。
大数定律根据收敛的条件分为强大数定律和弱大数定律。前者指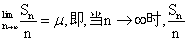绝对收敛于μ；后者指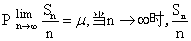依概率收敛于μ。

大数定律Laws of LargeNumbers

亦称“大数法则”。见“大数法则”。

大数定律

概率论的基本定律之一，指关于大量的随机现象具有稳定性质的法则。它说明，如果被研究现象的总体是由大量的相互独立的随机因素所形成的，而且每个随机因素对总体的影响都相对地比较小，这时对大量因素加以综合平均，上述因素的个别影响就将互相抵消并显现出它们共同作用的倾向，使总体具有稳定的性质。大数定律的涵义具体可归纳为以下四个方面：（一）现象的某种总体性规律，当将具有这种现象的足够多的单位加以综合汇总的时候，这种规律才能够明显地显示出来；（二）现象的总体性规律通常是以平均数的形式表现出来的；（三）所研究现象的总体包含的单位数越多，平均数也就越能正确地反映出这些现象的普遍规律性；（四）各单位的共同倾向决定着平均数的水平，而各单位对平均数的离差则会由于足够多数单位综合汇总的结果而相互抵消，表现为趋向于消失。就抽样推断而言，大数定律则证明：如果由随机变量构成的总体存在着有限的平均数和方差，则对于充分大的抽样单位数n(一般指n>30)，将会有几乎趋近于1的概率，期望抽样平均数与总体实际平均数的绝对离差为趋近于0。

大数定律

亦称“大数法则”。指随机现象在大量重复试验中出现的规律性。例如，抛掷一枚硬币，每次出现正面或反面是偶然的，但经过大量重复抛掷时，出现正面的次数必然接近于总抛掷次数的1/2，这个比例是相当稳定的。最早的大数定律为贝努里所发现。贝努里大数定律为： 设m是n次独立试验中事件A出现的次数，而P是事件A在每次试验中出现的概率，则对于任一正数ε，有

本式表示n足够大时，随机事件出现的频率m/n，就会接近于概率P，体现了频率的稳定性，这时可用频率代替概率。常用的大数定律还有车比雪夫大数定律： 设随机变量x1,x2……xn相互独立，且服从同一分布，其期望值E(xK)=μ，方差D(xK)=σ2，则对于任一正数ε，有

本式表示当n足够大时，总体期望值与算术平均数有较大偏差的可能性很小，这时可用算术平均值估计总体期望值。已经证明的大数定律还有普阿松大数定律、辛钦大数定律、马尔柯夫大数定律、柯尔莫哥洛夫大数定律等。

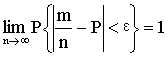
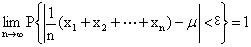
大数定律law of large numbers

亦称“弱大数理论”。概率论与数理统计学基本定律之一。揭示随机变量序列的算术平均数向某一常数趋近和收敛的定律。随机事件有些现在还没有发现其遵循的规律，但有些在大量重复出现条件下，呈现几乎必然的统计特性，即在不变的试验条件下，重复试验多次，随机事件出现的频率趋近于一个常数。如，向上抛一枚硬币，硬币落下后哪一面朝上是偶然的，但当上抛次数足够多，达到上万、几十万、几百万次以后，硬币每一面向上的次数约占总次数的二分之一，即每一面出现的概率为0.5。这种情况下，偶然中包含着必然。必然的规律与特性在大量样本中得以体现。