多项式的辗转相除法duoxiangshi de zhanzhuan xiangchufa

一种求最高公因式的方法.对于数域P上任意两个多项式f(x),g(x),g(x)≠0，在P上存在一个最高公因式d(x)，且d(x)可以表示成f(x),g(x)的一个组合，既有P上的多项式u(x),v(x)使

d(x)=u(x)f(x)+v(x)g(x).

由带余式除法，若g(x)≠0可以得到下面一系列等式

其中，g(x),r₁(x),r₂(x)，…的次数不断降低，有限步终止.r_s(x)就是f(x)与g(x)的一个最高公因式.存在c,(f(x),g(x))=cr_s(x).把这种求最高公因式的方法称为辗转相除法.
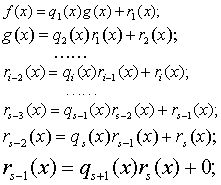
由以上等式的倒数第二个，有

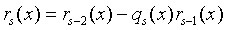
用它上面的等式逐个消去r_s-1(x),r_s-2(x)，…，r₁(x)，并加以整理就得到

r_s(x)=u₁(x)f(x)+v₁(x)g(x).

若d(x)=(f(x),g(x))，则d(x)=cr_s(x).