多组组合duo zu zuhe

把x个不同的元素分成m组，第一组有n1个不同的元素，第二组有n₂个不同的元素，………，第m组有n m个不同的元素，n₁+n₂+………+n_m＝n，这样不同的分组方法称为多组组合，其分组的种数记作

通常意义下的组合则是其特例。
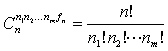
重复次数有限的排列问题可以转化为组合问题。例如，有n1个 “1”号球，n₂个 “2”号球，………，nm个“m”号球排成一排，则不同的排法相当于把n₁+n₂+………+n_m个位置分成m个组，第一组放“1”号球，第二组为 “2”号球，………，第m组放 “m”号球，因此排法数归结为上述分组方法数，即

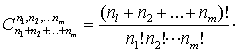
例如，12名新生安排在A,B,C三个宿舍，若A室住5名，B室住4名，C室住3名，问这12名新生全部分配方法有多少种？
若从乘法原理分析，可知从12名新生中选5名住A室共有C₁₂⁵种。对于其中每一种安排法，再从余下的7名中选4名住B室，有C₇⁴种。这样，共有C₁₂⁵·C₇⁴种。对于其中每一种安排法，再从余下的3名中选3名住C室，因此，共计分配方法有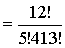种。
若从多组组合角度考虑，则第一组即是A室有5个新生，第二组(B室)有4名新生，第三组(C室)有3名新生。因此，共有分配方法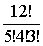种。
若n₁＝n₂＝………=n_m＝1，即n_l+n₂+………+n_m＝n，即是从n个不同元素可以有不同的分组方法数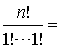n_!。实质上，这就是从n个不同元素全取的排列种数。