一元二次方程根与系数的关系

---

一元二次方程ax²+bx+c=0的两个根x₁，x₂与系数a，b，c存在如下关系：x₁+x₂=－b/a，x₁·x₂=c/a．

注意1．一元二次方程根与系数的关系也称为韦达定理．

2．一元二次方程根与系数关系，有以下几种常见的变形形式．

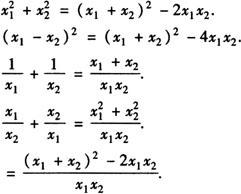
例1 已知一元二次方程x²－2x－1=0的两个根是x₁，x2，则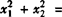＿＿，x₁－x₂=＿＿．

答 6，±2．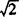

[解析] 由根与系数的关系，有x₁+x₂=2，x₁·x₂=－1，只要能用x₁+x₂，x₁·x₂来表示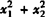，x₁－x₂，就可以实现由已知向未知的转化，所以得．

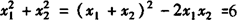(x₁－x₂)²=(x₁+x₂)²－4x₁x₂=8，即．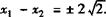

例2 已知方程3x²+2x－11=0的两根分别为x₁，x₂，则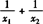的值是( )．

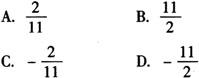
答 A．

[解析] 由根与系数关系，有

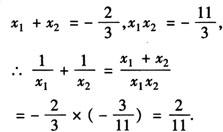
故选A．

例3 若x₁，x₂是一元二次方程2x²－3x+ 1=0的两个根，则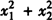的值是＿＿．

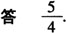
[解析] 由根与系数关系，有

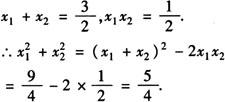
例4 已知一元二次方程x²+3x+1=0的两个根x₁，x₂，那么(1+x₁)(1+x₂)的值等于＿＿．

答 －1．

[解析] 由根与系数的关系：

x₁+x₂=－3，x₁x₂=1．

∴(1+x₁)(1+x₂)

=1+x₁+x₂+x₁x₂

=1－3+1=－1．