多因素肥料试验multifactorial fertilizerexperiment

含有两个或两个以上人为控制因素的肥料试验。在肥料试验中经常进行多因素试验。不同肥料施用于同一田块，肥料效应间往往发生相互影响。A肥料对B肥料产生的相互影响称为A与B肥料的交互作用效应，用AB表示交互作用项。多因素肥料试验可以计算出不同肥料之间或施肥与其他农业技术措施之间的交互作用效应，这是单因素试验所做不到的。
完全实施方案 在两个因素的肥料试验中，A因素的水平数k=1,2，…，a;B因素的水平数l=1,2，…，b；重复数j=1,2，…，r。该试验实验单元的处理数为a·b个，实验单元的总数为a·b·r个。如用随机区组设计，试验的线性数学模型为：
Y_jkl＝μ+ρ_j+α_k+β_l+(αβ)_kl+ε_jkl (1)式(1)中μ为总体平均，因素A、B及重复效应分别为α_k、β_l、ρ_j，交互作用效应为(αβ)_kl,ε_jkl为随机误差。只要在试验设计上保持各组合搭配完全就可计算得交互作用效应AB。
一个试验中人工控制的因素愈多，交互作用项也愈多。三因素试验中二因素的交互作用有AB、AC、BC三项，还有三个因素之间的高价交互作用效应ABC。四个以上因素的试验中交互作用项可根据式(1)拓广，其方差分析时各项平方和及自由度的分解也可仿式(1)拓广。式(1)是随机区组设计方案的线性数学模型，如采用拉丁方、裂区试验、混杂设计、平衡不完全区组等设计方案，则线性数学模型及平方和、自由度的分解亦需作相应的变动。
在完全实施试验方案中常用各因素水平数相乘来表示设计方案，如2×3×3、3×3×3分别表示两个三因素试验，第一个试验因素A为二水平，因素B、C为三水平；第二个试验的三个因素均为三水平。
部分实施方案 3×3×3试验方案中的处理组合数目为3³＝27。处理组合数随因素数与水平数而呈几何级数增加。如果试验规模扩大，不可能按完全实施方案试验，只能有计划地选择一部分处理方案进行试验，必须采用部分实施试验方案。由于肥料种类很多，有时还需考察肥料与其他因素的相关关系，常需进行较多因素的试验，因此部分实施试验方案在肥料试验中应用甚为普遍。
正交设计 用正交表安排的多因素肥料试验设计。正交表具有搭配均衡与整齐可比两个特点，根据试验目的和内容可选用适当的正交表。正交表有可以和不可以考察交互作用效应两种情况。其线性数学模型因试验内容不同，设计方法有很大变化。正交设计常用于快速求得较佳的肥料搭配组合，为下一阶段试验设计方案提供初步资料。
回归设计 回归设计是将回归分析原理用于多因素肥料试验设计，寻求实验单元少并具有良好统计性质的试验方案。回归设计试验用回归方程表达试验结果，近代肥料试验采用回归设计已较为普遍。应用得最多的是线性多项式数学模型和二次多项式数学模型

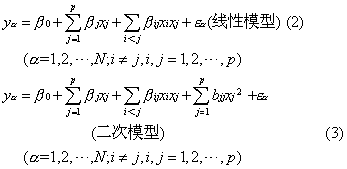
式(2)、(3)中y为试验数据，α为处理数目，x为因素，j为因素数目。用最小二乘法求出式(2)、(3)的各项参数，对回归方程进行显著性测验后求得各项肥料或其他因素各水平的优化组合。