复合映射
复合映射fuhe yingshe
设对于集合A,B,C有映射f:A→B和映射y:B→C,那么由法则(x)=g[f(x)](x∈A,(x)∈C)所确定的映射:A→C就叫做f与g的复合映射(如图).
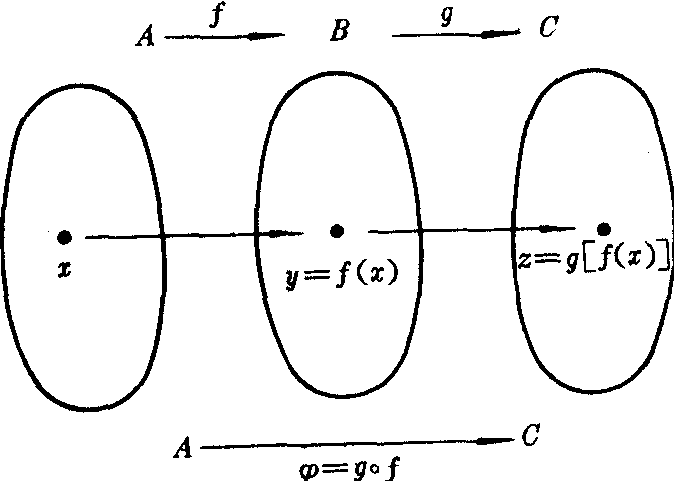
记作=g°f:a→C
上图直观地表示:通过第一个映射f:A→B,集合A中的任一元素x在B中有唯一的象y=f(x).再通过第二个映射:g∶B→C,在C中有y的唯一的象z=g(y),也就是说,A中的元素x通过中间元素y与C中的一个元素z对应,这种由A经过B到C的单值对应(映射)就是复合映射y=g◦f∶A→C.
一般地说,符号g◦f与f◦g是有区别的.例如,设映射f∶R→R由法则f∶x→y=x2(x∈R,y∈R)确定,g∶R→R由法则g∶y→z=siny(y∈R,z∈R)确定,则
g°f(x)=f[g(x)]=(sinx)2
f°g(x)=g[f(x)]=sinx2
因为(sinx)2不恒等于sinx2,所以f°g≠g°f.
☚ 到内映射 集合的等价 ☛
- 少先队队长方法手册是什么意思
- 少先队队长活动手册是什么意思
- 少先队队长管理手册是什么意思
- 少先队队长箴言手册是什么意思
- 少先队鼓号手小手册是什么意思
- 少先队鼓号队是什么意思
- 少免耕作业机具是什么意思
- 少公是什么意思
- 少共关中特区委员会是什么意思
- 少共国际师是什么意思
- 少共陕甘宁省委员会是什么意思
- 少共陕甘省委员会是什么意思
- 少关是什么意思
- 少兴是什么意思
- 少典是什么意思
- 少内是什么意思
- 少内啬夫是什么意思
- 少冈是什么意思
- 少再得,多则惑是什么意思
- 少冲是什么意思
- 少决断是什么意思
- 少凯是什么意思
- 少则得。是什么意思
- 少则得,多则惑是什么意思
- 少则有壮,壮则有老是什么意思
- 少则逃之是什么意思
- 少别是什么意思
- 少别千年是什么意思
- 少刻是什么意思
- 少剑是什么意思
- 少剑波是什么意思
- 少剑(见)是什么意思
- 少劳少得是什么意思
- 少勋是什么意思
- 少勍是什么意思
- 少勿来是什么意思
- 少包车是什么意思
- 少匠是什么意思
- 少匹肋巴是什么意思
- 少午是什么意思
- 少午些是什么意思
- 少午阵是什么意思
- 少午饭是什么意思
- 少半是什么意思
- 少半个(子)是什么意思
- 少半拉是什么意思
- 少华是什么意思
- 少华山是什么意思
- 少华甘露寺是什么意思
- 少华西来朝白帝,太行东望走黄河。是什么意思
- 少华集是什么意思
- 少南是什么意思
- 少卫是什么意思
- 少卿是什么意思
- 少卿事是什么意思
- 少卿应识子卿心是什么意思
- 少厂是什么意思
- 少原是什么意思
- 少叔是什么意思
- 少叫一声哥,多爬十里坡是什么意思