附丽;复利;富丽
◉ 附丽fùlì 书 动 依附;附着。〈例〉~权贵/ 无所~/ 希望是~于存在的/ 权责皆相~,宠信言事,不下于(敬)翔。〈近〉附着/ 依附。
◉ 复利fùlì 名 计算利息的一种方法,把前一期的利息和本金加在一起算做本金,逐期滚动计算利息。〈例〉~可观/ 计算~/ 把存折上的~取出来。
◉ 富丽fùlì 形 宏伟美丽。〈例〉~堂皇/ 陈设~/ 山崖上矗立着一幢巍峨而~的洋楼。〈近〉华丽。〈反〉简陋/ 简朴。
复利fù lì
计算利息的一种方法。将本金及其产生的利息加在一起算做本金,再计算利息。1914年朱执信《未来之价值与前进之人》:“今如以中国市场言,年息百分之八,每半年付息一度,此非甚高之利率也。然使有人提一钱(一圆之千分之一)而出之,以委诸公众,使无动其资本利息,而以复利法增殖之,则五百年之后,此所积者当在一百兆圆以上(万万为亿,万亿为兆)。”1917年俞子夷《江苏省立第一师范附属小学关于职业教育之过去未来》:“储蓄银行则仿照本地储蓄银行例,一律给利,亦照六个月一结之复利计算。”1931年《英汉对照百科名汇》:“Compound interest,复利。”
复利fù lìанатоц зм;слóжный процéнт
зм;слóжный процéнт
单利←→复利dān lì ← → fù lì
单利:只按照本金计算利息。
复利:将前一期的利息和本金合在一起算做本金来计算利息。
【例】 这笔借款按单利计算,不按复利计算。
复利
“单利”的对称。计算利息的一种方法。将所生利息加入本金再计利息,逐期滚算。俗称 “利上滚利”。计算公式为:
A=P (1+r)n
式中: A为本利和,P为本金,r为利率,n为期数。复利compound interest
存款或贷款在一定时期内所生利息加入本金再重复计算利息的方法。俗称“利上滚利”。计算公式为:A=P(1+r)n。式中A为本利和;P为本金;r为利率;n为期数。
复利
“单利”的对称。计算利息的一种方法。经过一定期间,将所生利息并入本金再计利息,逐期滚算,俗称“利上加利”。计算公式为:
A=P×(1+r)n
其中A为本利和,P为本金,r为利率,n为期数。复利Compound Interest
每经过一个计息期,将所生利息加入本金逐期滚算的计息方法。俗称“利滚利”。
复利
“单利”的对称。将经过一定时间所计算的利息并入本金而再次计算的利息。它需逐期滚动计算。复利的本金与利息之和(简称“本利和”)的计算公式为:
复利的本利和=本金×(1+利率)n
式中n为借贷期限。求复利的利息额,只要将其本利和减去本金金额。复利
“单利”的对称,计算利息的一种方法,经过一定时期 (如一年),将所生利息加入本金再计利息,逐期滚算。俗称“利滚利”。其计算公式:
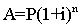
1669年,“现代银行业之父” 约瑟亚·柴尔德指出: “100镑按10%的利息率以复利计算,经过70年,就会生出102400镑”。18世纪英国经济学家理查·普莱斯更离奇地说: “生复利的钱,起初增长得很慢,以后就不断加快,过了一段时间之后,其速度就超出任何想象。一个便士,在耶稣降生那一年以5%的复利放出,到现在会增长成一个比15000万个纯金地球还要大的数目。可是如果以单利放出,在同样长的时间里,它至多只能变成7先令4 /CRFDPIC/r200703085/r200703085.1623.ea5db2.png便士。” 不过,马克思对普莱斯“把资本看作自动运动的自动机,看作一种纯粹的、自行增长的数字” 的评论是 “想入非非”,是 “荒诞无稽的幻想”,并且 “已经远远超过炼金术士的幻想。”
复利compound interest
亦称为“利滚利”。“单利”的对称。计算利息方法之一。将经过一定时间所计算的利息并入本金再次计算的利息,逐期滚动计算。其计算公式:
复利本利和=本金×(1+利率)n
式中,n为时间。复利Compound Interest
本金及其利息都同样计息的计算利息的方法。其计算公式为:
FV=PV(1+i)n
I=PV[(1+i)n-1]
其中:PV——原来的本金;i——利率;n——期数;FV——n期末的复利终值;(1 +i)n——复利终值因子,以(FV/PV,i,n)为其通用代号,其值可以从现成的复利终值表查得;I——本金n期的复利利息。
例如,某人存款5000元,年息率为5%,存款期为2年,则
FV=5000×(1+5%)2=5512.5(元)
I=512.5(元)
复利期 将一定期间内已获的利息加入本金所用的期间。通常以1年、半年、3个月、1个月或其他有规则的间隔期为复利期。以1年为复利期,即1年复利一次,复利期的利率就是年利率。以半年为复利期,即每半年复利一次,或1年复利两次,每一复利期的利率是年利率的1/2。以3个月为复利期,1年复利四次,每一复利期的利率是年利率的1/4,其余类推。
复利CompoundInterest
本金每期的生长数(报酬) 在期末加入本金并在以后各期内再计报酬的情况下,本金在两期或两期以上取得的报酬。国际间的项目投资及借款往往超过一期,投资者一般考虑的是一连串的定期报酬,每期报酬又可重复投资以获得更多的报酬,即利上滚利。因此,收益再投资使资本不断增长是经济现实中的一种共同现象。设S为复利,P为本金,r为利率,n为期数,则复利的计算公式为:
S=P[(1+r)n-1]
假定借款为10,000美元,期限为3年,年率为10%,每年计算一次复利,3年后归还本金,则复利应为:
S=10,000× [(1+0. 10)3-1]
=3,310美元
复利
“单利”的对称。利息计算的方法之一。指本金每期的生息数在期末加入本金并在以后各期内滚动再计利息。复利概念可包括复利终值、复利现值、年金终值和年金现值等内容。复利终值 (Com-pound Account) 又称复利的本利和或到期值,是指本金在约定的期限内按一定利率计算每期利息,并将其加入本金计算利息,逐期滚算到约定期末的本金和利息总值。其计算公式如下:
a=p (1+i)n
式中: a代表复利终值,p代表本金,i代表利率,n代表复利期数或计息期。例如,本金10 000元,年利率 8%,三年后的复利终值: a=10 000×(1+0.08)3=12 597元。复利现值 (Present Value)是指一定时期后一定金额的现在价值。它的意义与复利终值恰恰相反。终值是根据现在的投资金额、利率及经过的时间,计算投资在将来的价值。而现值则是通过将来达到的金额、利率和经过的时期,来测算现在须投资的金额。把未来金额折算成现值的过程称为贴现 (Discount)。复利现值的公式可由复利终值公式推出。即由a=p (1+i)n,可得:
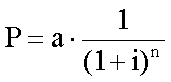
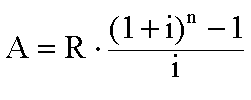
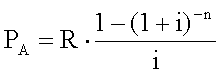
AD=R (A i-1)
i-1)
 i代表n+1期的普通年金终值, n、i含义同上。期初年金现值 (Present Value of an AnnuityDue) 指在今后一段时期内每期期初都有一笔等额收入或支付的现在价值之和。计算公式为:
i代表n+1期的普通年金终值, n、i含义同上。期初年金现值 (Present Value of an AnnuityDue) 指在今后一段时期内每期期初都有一笔等额收入或支付的现在价值之和。计算公式为:PD=R(P i+1)
i+1)
 i代表n-1期普通年金现值,R、n、i含义同上。复利的计算比较复杂,一般我们可借助于事先编好的复利表来备查。复利计算法是研究项目投资经由不同时间,以不同形态流入流出的现金价值时所采用的一种科学方法。西方国家银行长期借贷业务一般采取这种方法。
i代表n-1期普通年金现值,R、n、i含义同上。复利的计算比较复杂,一般我们可借助于事先编好的复利表来备查。复利计算法是研究项目投资经由不同时间,以不同形态流入流出的现金价值时所采用的一种科学方法。西方国家银行长期借贷业务一般采取这种方法。复利
compound interest
- 明矾解毒汤是什么意思
- 明矾(硫酸铜)是什么意思
- 明码是什么意思
- 明码实价是什么意思
- 明码标价是什么意思
- 明码电报是什么意思
- 明砍是什么意思
- 明砍(侃)是什么意思
- 明确是什么意思
- 明确一致是什么意思
- 明确上市规则是什么意思
- 明确公正的判断是什么意思
- 明确写作目的是什么意思
- 明确决定是什么意思
- 明确地分辨是什么意思
- 明确地区分是什么意思
- 明确地训诫是什么意思
- 明确完备是什么意思
- 明确意见是什么意思
- 明确承认是什么意思
- 明确承诺是什么意思
- 明确本节课教学目的的技能是什么意思
- 明确概念法是什么意思
- 明确班干部职责的技能是什么意思
- 明确理解是什么意思
- 明确的主张是什么意思
- 明确的准则、规矩是什么意思
- 明确的态度是什么意思
- 明确的愿望是什么意思
- 明确的文字记载是什么意思
- 明确的本分是什么意思
- 明确的见解是什么意思
- 明确的见识是什么意思
- 明确的道义准则是什么意思
- 明确目标记忆法是什么意思
- 明确而肯定是什么意思
- 明确肯定是什么意思
- 明确规定的期限是什么意思
- 明确认定是什么意思
- 明确,分明是什么意思
- 明硯是什么意思
- 明碧轩是什么意思
- 明礁是什么意思
- 明示是什么意思
- 明示与默示条款是什么意思
- 明示于众是什么意思
- 明示人民是什么意思
- 明示保证是什么意思
- 明示信托是什么意思
- 明示其一即排斥其他是什么意思
- 明示合同是什么意思
- 明示契约是什么意思
- 明示意思表示是什么意思
- 明示承认是什么意思
- 明示排斥默示原则是什么意思
- 明示的意思自治是什么意思
- 明示行为是什么意思
- 明社是什么意思
- 明祀是什么意思
- 明祖陵是什么意思