基尼系数Jīníxìshù

意大利经济学家科拉多·基尼创制的用来测量收入分配不平等程度的指标。系数数值0为收入绝对平均，1为绝对不平均，通常认为超过0.4为国际警戒线水平，表明贫富差距很大。

基尼系数jī ní xì shùкоэффициéнт Джни

基尼系数Jīní xìshù

意大利经济学家科拉夫·基尼提出的，用来测量社会收入分配平等程度的指标。
　❍ 我国自20世纪80年代起，～呈上升趋势，即不平等的程度在增加。　

相关链接

基尼系数是介于0与1之间的，0为收入支配完全平均，1为绝对不平均。在这区间的数值越小，收入越趋平均；反之，数值越大，收入分配差距越扩大。

基尼系数

用以衡量社会收入分配不均程度的指标。它是根据洛伦茨曲线计算的，即用积分的方法算出收入分配绝对平均线与实际收入分配线之间的面积，和实际收入分配线与下面边框（绝对不平均线）的面积，再计算出前者占后者的比例系数。其公式为：

基尼系数越小，表明分配的平均程度越高。基尼系数也是累进税论的分析工具。征收累进税和结合政府支出分配，能够改善社会财富的分配状况，即矫正社会的收入分配不均，表现在图中是使实际收入分配线尽量接近绝对平均线，从而缩小45。线与实际收入分配线之间的面积，而扩大实际收入分配线与绝对不平均线之间的面积，从而使基尼系数缩小，即促使社会分配公平化。事实上，这在资本主义社会的税收是根本做不到的。作为一种分析手段，洛伦茨曲线和基尼系数，在研究社会主义税负公平方面有一定参考价值。

基尼系数Gini coefficient

是指对收入分配平均程度的测度。由意大利几何和统计学家基尼 (corrade Gini)发明。具体指洛伦兹曲线和绝对平等线之间的阴影面积与绝对平等线以下的三角形面积 (三角形OAB，见图) 之比。基尼系数为0时，收入绝对平均； 基尼系数为1时，收入绝对不平均。一般情况下，基尼系数介于0与1之间。基尼系数越小，越接近于收入平均，反之则不平均。基尼系数可以用来检验财政收支 （包括税收和政府支出）究竟在多大程度上影响社会的收入分配或财产分配以及它们究竟是促进社会收入分配或财产分配的平均还是加剧了其不平均。如纳税前后的基尼系数之比可以用来判断税收的收入分配效应； 政府增加职工教育支出前后的基尼系数之比可以判断职工教育支出的收入分配效应。应予以注意的是基尼系数只是对相对值的一种量度。此外，一种收入分配在前一范围可能较另一种分配更为平均，而在后一范围则可能更为不平均，但两者可能有同样的基尼系数。

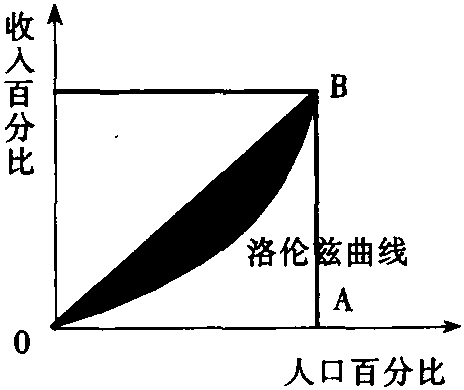
基尼系数Gini Coefficient

亦称“洛伦茨系数”。是20世纪初意大利经济学家基尼，根据洛伦茨曲线所定义的判断收入分配公平程度的指标。该系数是比例数值，在0和1之间，是国际上用来综合考察居民内部收入分配差异状况的一个重要分析指标。基尼系数最大为1，最小为0。前者表示居民之间的收入分配绝对不平均，即100%的收入被一个单位的人全部占有；而后者则表示居民之间的收入分配绝对平均，即人与人之间收入完全平等，没有任何差异。但这两种情况只是在理论上的绝对化形式，在实际生活中一般不会出现。因此，基尼系数的实际数值只能介于0—1之间。

基尼系数

又称“洛伦茨系数”。测量收入分配不平等程度的一种统计指标。由意大利经济学家基尼(Gini,Corrado,1884—1965)根据洛伦茨曲线的基本研究方法提出。参见“洛伦茨曲线”。

基尼系数

基尼系数是在洛伦茨曲线的基础上发展出来的一个综合度较高的收入分配状况指数，通过计算洛伦茨曲线图中洛伦茨曲线与对角线之间的面积以及对角线右下方的直角三角形面积，这两块面积相除所得的商即为基尼系数。如图，用公式表示：

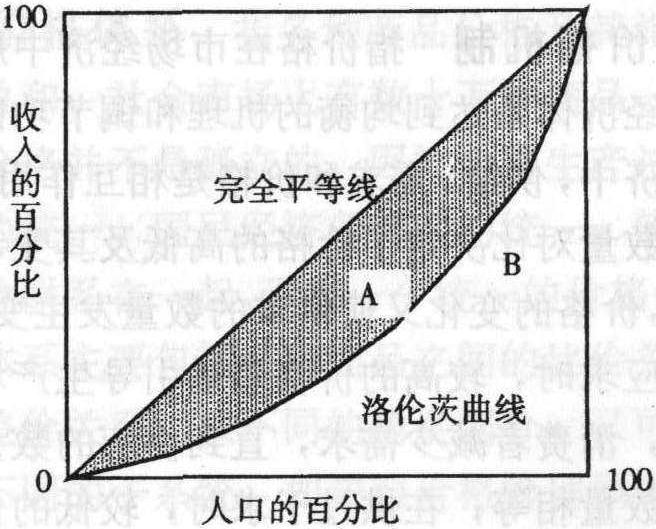
基尼系数=A/ (A+B)
基尼系数主要用来分析分配规模格局不平等的程度，这种方法是意大利统计学家C·基尼在1912年首次推出的，因此这一比率被称为“基尼稠密度系数”，简称基尼系数。基尼系数是不平等的标志，从0到1的变化区间内，基尼系数的值越大说明越不平等。基尼系数等于0，表明收入分配绝对均等；基尼系数等于1，表明收入分配绝对不均等。在具体通过基尼系数反映收入差距的状况时，一般认为，基尼系数在0.2以下表示绝对平均，在0.2～0.3之间表示比较平均； 0.3～0.4之间较为合理； 0.4～0.5之间为差距较大；0.5以上收入差距相当悬殊。

基尼系数

用来反映一个国家或地区不同时期收入分配的差异程度。基尼系数是根据分组资料计算的，等于实际收入分配线与绝对平均线所夹面积之比。基尼系数等于0时收入分配绝对平均，等于1时收入不平均，介于0.2和0.6之间为合理范围，小于0.2时过分平均化，大于0.6时收入分配差距过分悬殊。

基尼系数Gini Coefficient

是测量收入分配不平等程度的统计指标，在20世纪初由意大利经济学家科拉多·基尼 (Korrado Gini) 根据洛伦茨曲线的基本研究方法而提出来的，故名。
洛伦茨曲线如图所示：

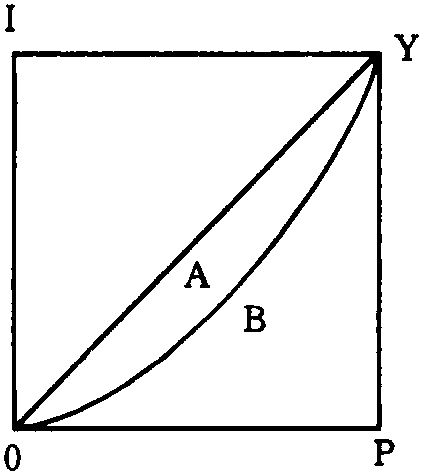
图中：OI表示收入百分比，OP表示人口百分比，联接两对角的直线OY (45°)是绝对平均曲线，OPY是绝对不平均曲线，在OY与OPY之间的曲线是实际收入分配曲线，即洛伦茨曲线，实际收入分配曲线是介于绝对平均曲线与绝对不平均曲线之间的。
根据洛伦茨曲线图示，A表示实际收入分配曲线与绝对平均曲线之间的面积，B表示实际收入分配曲线与绝对不平均曲线之间的面积。要判断实际收入分配的不平等程度，则需要比较A在绝对平均曲线以下的整个三角形面积 (A+B) 中的比例，这两部分面积之比，就是基尼系数，即：

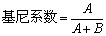
如果A=0，则基尼系数为0，收入绝对平均； 如B=0，则基尼系数为1，收入绝对不平均。
从理论上讲，基尼系数可以在0和1之间取值，但在实际上，它的取值范围一般在0.2～0.6之间，按国际上多年测量的数据，基尼系数在0.3～0.4之间为中等不平等程度。我国在改革开放前，由于实行平均主义、大锅饭的分配体制，基尼系数过小，例如，据世界银行估计，1978年我国城镇居民个人收入的基尼系数为0.16，这在当时几乎是世界上最低的，改革开放后，我国开始实行“允许一部分人先富起来” 的政策，收入差距迅速拉开，基尼系数以较快的速度上升，例如，据有些学者估计，我国城乡居民个人收入的基尼系数，1988年为0.382,1994年为0.434 (李强等，1995)，超过了美国战后基尼系数最高年份的数值0.430，数据表明，我国现阶段的基尼系数已超过了国际上公认的中等贫富差距的程度，可见，在改革开放以来的短短十几年时间内，我国就从一个收入差距最小的国家迅速转变为超过了世界上收入差距中等的国家，这种超常的变化，已使社会收入分配不公成为我国现阶段一个引人注目的社会问题，它不仅挫伤了相当一部分人的积极性，影响了我国经济效率的增长，而且也会对社会的安定造成潜在的威胁。如何分析收入分配不平等对社会安定的影响，是我国面临的一个现实问题。厉以宁提出，可以用基尼系数和社会平均综合收入满意度结合起来考察收入分配差距和社会不安定之间的关系。为此，可将基尼系数和社会平均综合收入满意度由高到低分依次为1级、2级、3级等，基尼系数越大，或社会平均综合收入满意度越低，则级别越高。一般说来，当基尼系数为1级，社会平均综合收入满意度为1级时，收入分配差距对社会安定产生的不利影响最大，这时可以把收入分配差距看成是造成社会不安定、社会动荡的主要原因，造成社会不安定、社会动荡的其他原因相形之下退居不重要的地位。而当基尼系数为3级，社会平均综合收入满意度为3级时，这时社会不安定可能主要由其他因素所引起，至少是由其他因素和收入分配差距共同引起的。(1995,P.37～39)
基尼系数作为测量收入分配不平等程度的一个指标，具有简单明了、综合性强等优点，但它在使用过程中也存在一些问题。马尔科姆·吉利斯等人认为，基尼系数存在的问题之一是各种洛伦兹曲线可能相交，以致不同形状的曲线可产生相同的基尼系数。问题之二是参考标准的绝对性质，使得基尼系数对分配的变化普遍很敏感，特别是对低收入集团的收入变化，敏感性最大 (1989,P. 99)。厉以宁认为，西方经济学家在使用洛伦兹曲线和基尼系数时公开或隐含地把“收入均等化”作为衡量收入分配合理程度的标准，这不适用于我国，在我国运用基尼系数时应有一条适用于我国的合理的收入分配曲线，这条曲线既不是绝对平均线也不是绝对不平均线，而是一条介于两者之间的曲线。并设想，我们可以打开思路，跳出洛伦兹曲线和基尼系数的框架，另外去探寻一个符合我国实际情况的衡量收入分配合理性的研究方法，寻找一种可以表明收入分配合理程度的指标或指标体系。除了基尼系数外，还有其他一些衡量收入分配不平等程度的指标，如库兹涅茨提出了一种“库兹涅茨比率”，把各层次的收入份额与人口份额之间的差相加起来，然后再除以人口数。这种方法运用在规模分配时，所反映的接近分配中心的不均匀性要比基尼系数大。

基尼系数Gini Coefficient

又称洛伦茨系数，衡量收入分配不平均程度的指标。20世纪初由意大利统计学家基尼(Corrado Gini)根据洛伦茨曲线提出。给定洛伦茨曲线I=I (P)，式中P=人口百分比，I=收入百分比 （如图）。图中45°线I=P表示收入分配绝对平均的洛伦茨曲线。基尼系数G为：

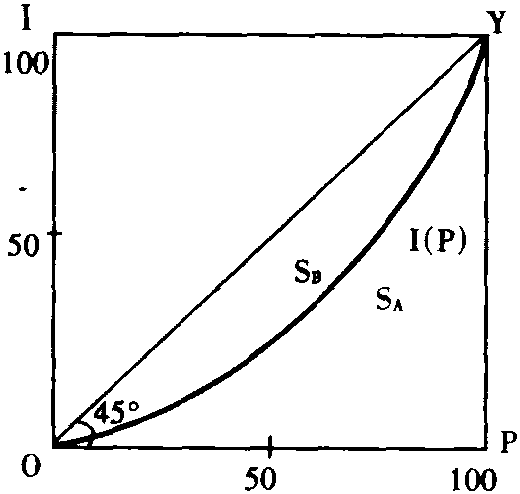
45°线和实际洛伦茨曲线

其中0≤G≤1。若G=0，实际洛伦茨曲线与绝对平均曲线重叠，表明收入分配是绝对平均的。若G=1，实际洛伦茨曲线与绝对不平均曲线重叠，表明收入分配是绝对不平均的。G愈接近于零，表明收入分配越平均；反之，愈接近于1，收入分配越不平均。批评基尼系数的人认为，概括性的统计数据可能没有完整的反映整个曲线的性质，并且基尼系数是一个不灵敏的、难以准确计算的、缺乏规范内容的尺度。但这一尺度仍然被广泛地应用于比较不同国家的收入分配和财产分配的平均程度以及政府税收（或政府支出）的收入分配效应分析等方面。其生命力恰恰在于洛伦茨曲线的直观性上。
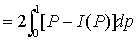
〖参〗 洛伦茨曲线

基尼系数

指在全部居民收入中用于非平均分配的百分比 。它是国际上通用的反映居民之间收入差异程度的指标。居民全部收入由平均分配和非平均分配两部分构成，平均分配部分不能反映居民收入的差异，只有非平均分配部分才能反映居民收入的差异。基尼系数的大小，就是反映全部收入中用于非平均分配的百分比的大小，即居民收入差异程度的大小。它最小等于零，表示居民收入分配绝对平均，毫无差异； 它最大等于1，表示居民收入分配绝对不平均，即百分之百的收入被一个人占有，这是不可能的。因此，基尼系数一般介于零与1之间。一般国家的基尼系数在0.2至0.6之间，低于0.2和高于0.6均属不合理。我国农民收入的基尼系数可划分为四个区间： (1)在0.2以下，为高度平均；(2)在0.2至0.3之间，为相对平均；(3)在0.3至0.4之间，为比较合理； (4)在0.4以上，为差距偏大。因此，作为宏观决策的经济参数，其调节区间在0.2至0.4之间为宜。

基尼系数Gini coefficient

以洛伦茨曲线为基础对分配不均等程度的一种概括性计量，具体来说，基尼系数等于洛伦茨图形中由对角线和分配不均等曲线所围之面积与对角线下部整个三角形面积的比率(参见“洛伦茨曲线”词条中所附图形，基尼系数等于A/(A+B))。显然，基尼系数越小，所显示的分配不均等程度便越小，反之则表明分配不均等程度的增大。一般认为，对于大多数发达国家，基尼系数约为0.4左右。这种计量方法是由意大利统计与人口统计学家柯罗多·基尼(Corrodo Gini)发明的，故命此名。
虽然洛伦茨曲线很少遇到争议，而基尼系数却遭到很多批评。首先，将整个曲线概括为一个单一比率也许会导致对于现实的误解。此外，这一系数具有不敏感的特征，很难被精确地计算和避免规范方面的因素。不过，此种计量仍然被广泛应用于描述不均等的概括性统计分析中。参见“洛伦茨曲线”。

基尼系数Gini coefficient

表示社会中收入分配不平等的程度。它根据洛伦兹曲线导出（如图），基尼系数G=A/A+B，其取值范围为0到1之间。若G=1，则表示社会收入分配绝对不平等，即占社会总人口99.99%的人所获得的收入为0，而全部社会收入都分配给一个人所有；若G=0，则表示社会收入分配绝对平等，即任意占社会总人口1%的人所获得的收入正好也占社会总收入的1%，这种

情况在图中表示为OX线，它呈45°；若G为0到1之间的一个数，则表示社会收入分配处于绝对不平等和绝对平等之间。

---

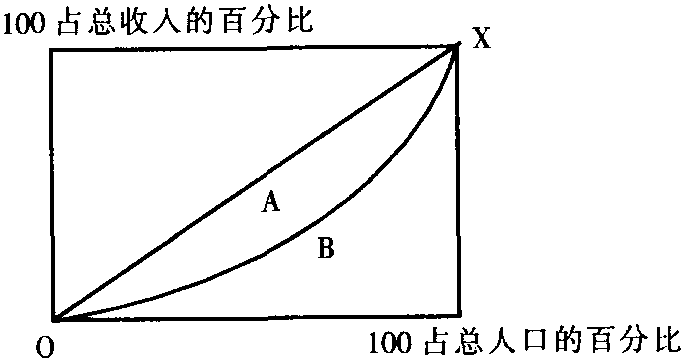
基尼系数Gini coefficient

参见“微观经济学”学科同名条。

---

基尼系数Geni Coefficient

参见“微观经济学”学科同名条。

基尼系数

参见“洛伦茨曲线”。