均值-方差资产组合分析meanvariance portfolio analysis

由马科维茨(Markowitz,1959)发展的一种特殊而有重要应用的资产组合选择方法。它假设投资者的效用由资产组合P的回报均值_p和回报的方差σ_p²决定，即效用函数形如v(_p,σ_p²)，且v₁>0和v₂<0，此处下标表示对第一、二个变量求偏导数。这意味着投资者认为_p越大越好，σ_p²越小越好。考虑n种资产，记资产i的回报为_i,i=1,2，…，n。 投资者把全部资金分别投入到这n种资产上，设投到资产i上的资金占总资金的份额为w_i，则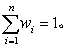称向量(w₁，…，w_n)为一个资产组合。此资产组合的回报为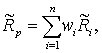从而组合的期望回报和方差分别为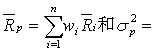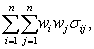其中σ_ij是R_i和_j的协方差。
在上述假设的效用函数下，备选的最优资产组合必定具有性质：对一个给定的方差水平，它有最大的期望回报，同时，对一个给定的期望回报水平，它有最小的方差，具有这种性质的资产组合称为均值一方差有效的。如果仅要求对一个给定的期望回报水平，有最小方差，则称它为最小方差资产组合。
从数学上求最小方差资产组合可写成解：

minσ_p²,s.t._p＝K

求有效均值—方差组合可写成解

max _p,s.t.σ_p²＝L

令K和L连续变化，就求得最小方差资产组合的集合和有效均值—方差资产组合的集合。可以证明，最小方差资产组合的集合是σ_p-坐标平面上的一条双曲线的一支，有效均值—方差资产组合的集合则是这一支的上半支。投资者按自己的偏好在这上半支选择投资组合。