图解法

体操术语记写法之一，是用连续图说明动作。它的特点是直观，运用方便。一般用于编写教案。在实际运用中往往把完整记写法与图解法并用。如：体操教材、体操等级大纲和广播体操图解等。

图解法

指把句子结构用图形表示出来，对句子进行分析的一种方法。此种方法曾是西方法语法学界流行的一种教学的辅助手段，黎锦熙《新著国语文法》引进用来分析汉语句法。如：

横线以上为句子的主要成分 (主语、述语) 以及述语的连带成分(宾语、补足语)，横线以下是句子的附加成分(形容词的附加语、副词的附加语)。主语和述语之间用双竖线表示，述语及其连带成分之间用单竖线表示。形容词的附加语线向左，副词的附加语线向右。后来使用图解法的人在此基础上进行了一定的改造。参见“层次图”。

图解法

系直接由可行解集合的图形中找出最佳解的方法。即线性规划模型中当决策变量不超过两个时的一种单纯形解法。用图解法解线性规划问题一般分两步完成： 第一步，寻找可行解。将所有约束条件都变成等式，然后将其图示在平面直角坐标上，找出由这些约束条件所构成的公共域，该公共域即为可行解域，凡落在该区域的所有方案均为可行方案； 第二步，在可行方案中寻求最优解。令目标函数Z等于零，然后将其图示在平面直角坐标上，接着将该目标函数线脱离原点向上平行移动，依次与可行解域折线拐点相交。根据线性规划原理，最优解只能是其中一个拐点。如果目标函数是求极小值，那么最先与平移目标函数线相交的拐点坐标即为最优解，因为此点离原点最近； 反之，如果目标函数是求极大值，那么最后一个与平移目标函数线相交的那个拐点即为最优解。

图解法

利用图形求解线性规划问题的一种方法。这种方法一般只适于两个变量的简单模型。首先由丹捷格于1951年提出，到1953年由霍夫曼等人加以详述。其基本思想和程序是先画出由约束条件所确定的可行解集，再在可行解集中找出一个能使目标函数达到最大值的最优解。例如：
求x1,x2的值，使它们满足

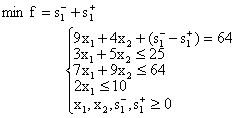
并且使目标函数

S=2x₁+5x₂

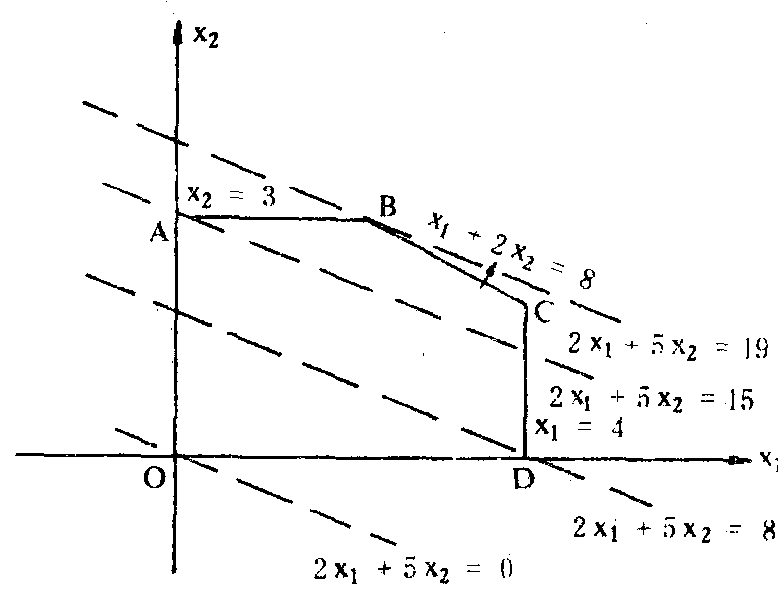
的值最大。
解： 如果把x1,x2看成坐标平面上点的坐标，那么满足约束条件中每一个不等式的点集就是一个半平面。因为约束条件是由五个不等式组成的，所以满足约束条件的点集是五个半平面的相交部分，即下图中凸多边形OABCD上任何一点的坐标，都同时满足约束条件中的五个不等式。而其外的任何一点的坐标都不能同时满足这五个不等式。所以凸多边形OABCD上的每个点的坐标都是这个线性规划问题的一个可行解。这个凸多边形上点的全体构成这个线性规划问题的可行解集。为使目标函数取得最大值，令S=0，那么，2x1+5x2=0是坐标平面上的一条直线。这种直线上任何一点的坐标值都使目标函数取值相等的直线，被称之为等值线。若再令S分别为8、15、19作平行直线簇，由图中可以看出，当直线离原点愈远时，S值愈大。因此，图解法的最后问题是要在上列平行线中，找出一条直线，使之既与凸多边形OABCD相交，而又尽可能远离原点。这种既满足约束条件，且使目标函数取得最大值的点 (如图中的B点) 的坐标，即为最优解。B点的坐标通过解联立方程：

得最优解为x1=2; x2=3。相应的目标函数的最大值为： S=2×2+5×3=19

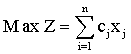
图解法