图形问题Tuxingwenti

数和图形是数学研究的两类基本对象，它们之间的关系密不可分。一方面，一个图形有自身的几何与数量特征，另一方面，图形又是表现数量之间的关系的有力工具。图形问题有助于学生的数学形象思维， 有助于培养学生的空间想象力以及从直观的具体的事物中抽象出一般概念和规律的能力。
例1 （首届华罗庚金杯赛复赛）: 甲、乙、丙、丁与小强五位同学一起比赛象棋，每两人都要比赛一盘，到现在为止，甲已经赛了4盘，乙赛了3盘，丙赛了2盘， 丁赛了一盘， 问小强已经赛了几盘？
解：这一问题可以利用“关系图”的方法解决，用五个点代表五位同学，如果两人已经赛过，就在对应两点之间连一条线。那么，根题意，甲已经赛了4盘，甲到其余4点都有连线，乙赛了3盘，而丁只赛了一盘，故乙到丁以外各点都有连线。于是得到下面的图。在这张图中，有4条线与甲相连，连接乙、丙、丁的线分别有3、2、1条，符合题目要求。连接到小强的线有两条， 所以小强已经赛过两场。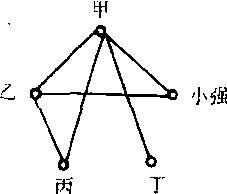
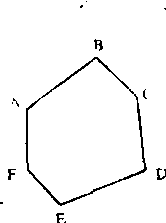
例2: 假定如图的六边形的任意三条对角线不交于一点， 试问在六边形内部共有多少个对角线交点。
解：问题是由图形导出的，但如拘泥于直观的办法——把所有对角线画出来，一个个地去数它们的交点，不仅麻烦，而且易错。换一个角度考虑，不难看出：任取六边形的四个顶点，恰有以它们为端点的一对对角线在六边形内部相交，这就是说， 六边形的每四个顶点决定唯一一个对角线交点，因此，在六边形内部的对角线交点个数可组合计算， 即C46=15个。
这个问题可以推广到一般情形： 假设凸n边形的任意3条对角线不交于内部一点， 则在此凸n边形内部， 对角线交点个数为C4n个。
通过以上二例可以看出：有的数学问题，借助于图形能够获至简单明了的解答。而在另一些情形下，则需要抽出图形的内在数量关系， 借助一定的数学工具去解决图形问题。