回归分析法

根据事物内部的因果关系及其发展的内在规律，用以解决事物发展内部变量之间相关关系的数学方法。对未来事物的发展作出科学的估计。服务于决策。

回归分析法

亦称“相关分析”。是处理变量之间关系的一种数学方法。在企业生产经营活动中经常需要处理各种事物的变量关系。如产品产量、质量、成本、利润、物资消耗等等之间的变量关系。它们之中，一个变量的变化（自变量）往往与另一变量 （因变量）之间存在内在的联系，或者是同向变化，或者是反向变化通过从大量的数据之中揭示其变化规律，就要采用回归分析法： 回归分析法的主要做法是：
(1)确定几个变量之间是否存在相关关系，并从而找出它们之间的数学模式；
(2)根据数学模式预测和控制变量间的相互变化数值；
(3)对各种影响因素进行定量分析，找出主要影响因素。应用回归分析法进行预测，必须建立回归方程，根据事物之间关系的复杂程度，回归方程分为多种类型，当相关关系的统计规律（可用坐标图观察）呈线性关系时称为线性回归，反之，称为非线性回归，线性回归中，自变量是一个，称为一元线性回归，自变量是多个，称为多元性回归。企业在进行回归分析时，要根据分析对象采用相应的方法。

回归分析法Method of Regression Analysis

从被预测变量和与它有关的解释变量之间的因果关系出发，预测经济过程未来发展的一种定量方法。当事物之间具有确定关系时，变量间就表现为某种函数关系。而有些事物，虽然它们之间有着密切的联系，但并不能准确地用一个函数确定事物间的关系，例如年级与学生年龄间的关系，虽然有年级越高，年龄越大的趋势，但并不能由年级精确的确定学生年龄，这种事物间不确定的关系称这些事物间具有相关关系。具有相关关系的变量虽不能用准确的函数把它们之间的关系表达出来，然而却可以通过大量的实际数据的统计分析，找出各相关因素的内在规律，从而近似地确定出变量间的函数关系。这是回归分析的基本思想与方法。回归分析法包括一元线性回归分析、多元线性回归分析以及非线性回归分析。回归分析法以事物发展的因果关系为基础，因而一般较准确。举例说明如下：
某地区从1991～1995年的化肥用量与作物产量如表11-5:

表11-5

年份	化肥用量X（万吨）	作物产量Y（亿公斤）
1991	15.0	39.4
1992	25.8	42.9
1993	30.0	41.0
1994	36.6	43.1
1995	44.4	49.2

为了研究相互关系，可先绘图分析(见图11-7)。

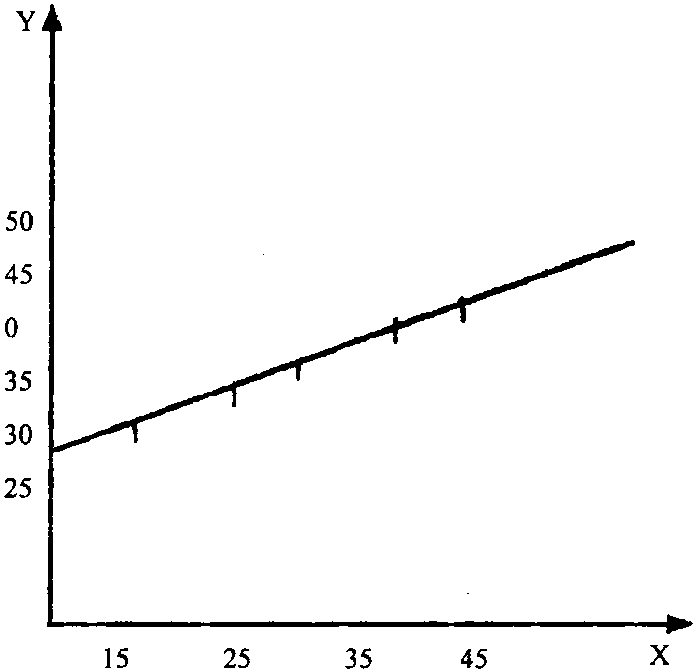
图11-7

由图11-7可假设X与Y的关系为Y=a+bX,a、b为待定参数。按最小二乘法求a、b。
设X为X值的平均，Y为Y值的平均，则

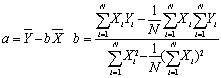
将上例数据代入可得a=34.32,b=0.29
所以回归关系方程为：Y=34.32+0.29X。

回归分析法

regression analysis