回归分析中的显著检验The Significant Test in the Regression Analysis
检验回归分析中的假设的一种方法,即利用样本资料去证实原假设是否真实。在这个程序中,需要构造一个检验统计量。最终根据从样本资料中计算出来的检验统计量的值决定接受原假设还是拒绝原假设。对于一元线性回归模型,在正态分布假定下,统计量为:
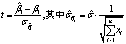
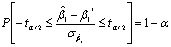
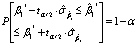
 有1-α的概率保证落在其中, 如
有1-α的概率保证落在其中, 如 1落在这个区间之外, 小概率事件发生了,此时将拒绝原假设。在实际应用中,当统计量t<-tα/2或t>tα/2,就拒绝原假设。对于二元及多元回归模型,在ui服从正态分布的假定下, 可以证明,
1落在这个区间之外, 小概率事件发生了,此时将拒绝原假设。在实际应用中,当统计量t<-tα/2或t>tα/2,就拒绝原假设。对于二元及多元回归模型,在ui服从正态分布的假定下, 可以证明, 0,
0,  1, …,
1, …, k也都是Yi的线性函数, 也是服从正态分布的随机变量。这样利用σ2的无偏估计
k也都是Yi的线性函数, 也是服从正态分布的随机变量。这样利用σ2的无偏估计 2代入各自的方差, 它们将都是服从自由度为n-k的t分布的随机变量,即
2代入各自的方差, 它们将都是服从自由度为n-k的t分布的随机变量,即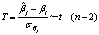
- 王龙才是什么意思
- 王龙泽是什么意思
- 王龙溪是什么意思
- 王龙溪全集是什么意思
- 王龙石是什么意思
- 王龙谿是什么意思
- 王龟谋是什么意思
- 王龟谋奉使日本是什么意思
- 王龟龄是什么意思
- 王(打字一)虔是什么意思
- 王𠪙是什么意思
- 王𢶏是什么意思
- 王𤴨是什么意思
- 王𨒿斌是什么意思
- 王𩔪是什么意思
- 王𰍻𰍻是什么意思
- 玌是什么意思
- 玍是什么意思
- 玍
.jpg)
.jpg) 是什么意思
是什么意思 - 玍七码八是什么意思
- 玍七马八是什么意思
- 玍不溜秋是什么意思
- 玍了是什么意思
- 玍们是什么意思
- 玍伧是什么意思
- 玍佞是什么意思
- 玍倯是什么意思
- 玍儿是什么意思
- 玍儿巴七痨是什么意思
- 玍儿杂子是什么意思
- 玍其混是什么意思
- 玍劲儿十足是什么意思
- 玍古是什么意思
- 玍古天道是什么意思
- 玍古蛋子是什么意思
- 玍古话是什么意思
- 玍固是什么意思
- 玍头是什么意思
- 玍子是什么意思
- 玍小子是什么意思
- 玍扎是什么意思
- 玍扎子是什么意思
- 玍拉古东儿的是什么意思
- 玍拉玍七是什么意思
- 玍拧是什么意思
- 玍朵子是什么意思
- 玍杂是什么意思
- 玍杂子是什么意思
- 玍核是什么意思
- 玍核子是什么意思
- 玍毛是什么意思
- 玍气十足是什么意思
- 玍油子是什么意思
- 玍牙子是什么意思
- 玍牛牌气是什么意思
- 玍玍是什么意思
- 玍脬是什么意思
- 玍话是什么意思
- 玍里巴是什么意思
- 玍骨是什么意思