回归分析huigui fenxi

“回归”原是生物学的词汇。英国科学家F·高尔顿在研究中发现：父母的身高与其子女的身高有一定的关系，即子女的身高向其父母的平均身高方向趋近，这种趋近现象称为“回归”。后来以此名词泛指变量间的这种关系。变量之间的关系一般可分为两类。一类是一种完全确定的关系，即称函数关系，如圆面积A与半径R的函数关系为A=πR2。另一类是一种不完全确定的关系，即称相关关系，如身高与体重的关系中，一般说来身高者体也重，但也有身高者体并不重的。在教育上较多的是相关关系。回归分析就是处理多个变量间相关关系的一种数学方法，它主要解决：
❶确定几个特定变量之间是否存在相关关系？如是，则要找出它们之间的合适数学表达式；
❷根据一个或几个变量的值，预测或控制另一个变量的取值，并要知道这种预测的精确度；
❸进行因素分析，找出主要变量和次要变量等。
回归与相关有联系也有区别。相关表示两个变量之间的双方向的关系，而回归表示一个变量随另一个变量变化的单方向的关系。
回归分析的主要内容有一元线性回归、二元线性回归和多元线性回归等。其中的“元”是指自变量的个数。这里着重介绍一元线性回归。
一元线性回归直线的计算 假定变量X与Y之间存在某种相关关系，而我们想以变量X来估计Y；这时X为自变量，Y为因变量。通过实验或观测，我们可以找到关于X与Y的若干数据；然后通过这些数据找到一条能描述这两个变量间关系的数学表达式（亦称经验公式）。若它们的关系是呈一直线，则称为一元线性回归直线。其一般形式为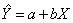

式中 Y——X的估计值
a和b——回归方程的常数项和回归系数。其中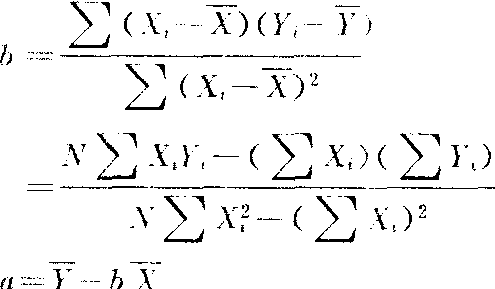

式中 N——数据(X₁,Y₁)的对数
[例1] 某中学12个学生的初二和初三的数学统考成绩如下。求其回归方程。

初二	63	53	52	58	88	60	62	56	76	55	90	49
初三	60	50	71	57	98	67	87	47	87	71	96	51

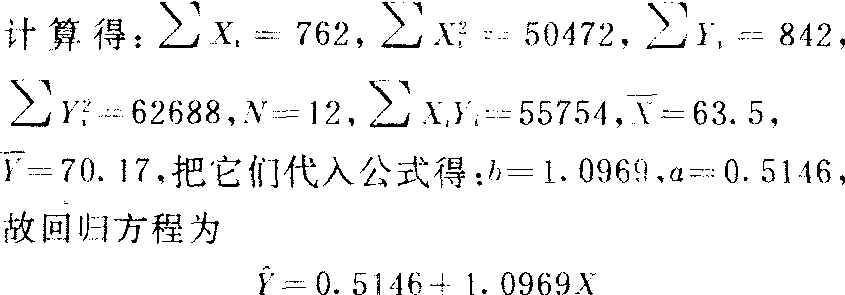
回归方程的效果 这个问题具体指：
❶回归系数b是否显著？若显著，则回归或预测效果较好。
❷回归效率有多大？即能被预测的成分占总成分的比例有多少。为此必须先对回归方程进行统计检验。检验的方法是对回归方程进行方差分析，即把因变量(Y)之间的总变差(SST)分解成自变量(X)之间的变差(SSU)和剩余变差(SSQ):

SST=SSL+SSQ

式中 SSU——回归平方和，属一种预测的变差
SSQ——剩余平方和，属一种非预测的变差
它们的方差分析表如下：

a=0.01及f₁ =1和f₂＝ 10查F分布表得F(1.₁₀₎₀.₀₁＝10.0。由F>F(1,₁₀)_0.01＝10，故拒绝假设H₀，即回归方程的回归系数有极显著的意义，亦即回归方程的效果很好。
回归方程的效率是回归变差在总变差中所占的比重，即

式中 r——相关系数
其余符号同前。
从式中亦可知，回归效率恰为相关系数的平方。
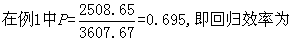69.5%。
注意：如果F检验不显著，则有下列几种可能：
❶影响Y的因素除X外，至少还有一个不可忽视的因素；
❷X和Y是非线性关系；
❸X与Y无关。
利用回归方程进行预测 从统计观点来看，所谓预测就是一个区间估计问题。即在回归方程中，在一定的置信水平α下，找出一个正数δ，使得某自变量X₀所对应的实际观测值Ŷ₀以(1-α)的概率落在(Ŷ₀-δ,Ŷ+δ)之内，即
或
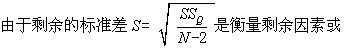
称随机因素波动程度的指标。显然，S愈小即随机因素的波动愈小，则对Y₀的预测就愈准确(即估计值Y0愈接近于Y₀)。因此S是回归方程中预测Y₀的精确度的指标。设X₀来自于正态分布，则它所对应的Y₀和Y₀也服从于正态分布，因而Y_0-Ŷ₀也服从于正态分布。这就是说，当X=X₀时，实际观测值Y₀是以估计值Ŷ₀为中心而正态地分布着，并且它与S之间有下述关系：
Y₀落在Ŷ₀±S内的概率约为0.683(68.3%);
Y0落在Ŷ₀±2S内的概率约为0.954(95.4%);
Y0落在Ŷ0±3S内的概率约为0.997(99.7%)。
就一般而言，Y₀落在下面二直线之间的概率为1-a:

故Y₀落在这2条直线内的概率为95%以上。
多元线性回归的方法与一元线性回归的思想基本相同，其回归方程为
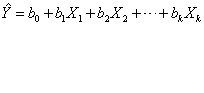
任何两个变量之离差积的平方和为

则关于b₁,b₂，…，b_k的正规方程组为

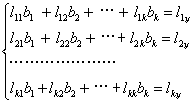
解这一正规方程组可得：b₁,b2，…，bk;

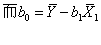
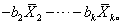
多元线性回归的方差分析表如下：

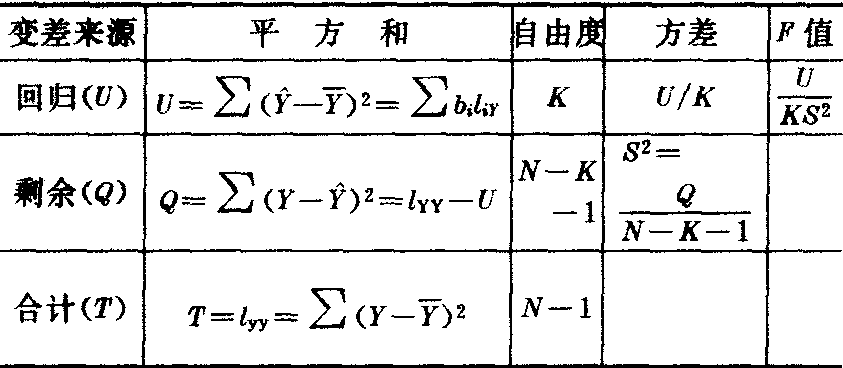
检验多元线性回归的效果是用复相关系数：

K2为回归效率。R与相关系数r的意义相同，但0≤R≤1；其检验方法亦与r相同，但自由度为N-K。

回归分析huigui fenxi

根据变量间的数量关系的模型来预测其中一些变量的状态的方法。由于描述、预测和控制是心理学研究的主要目的，因此，作为预测方法之一的回归分析具有很重要的意义。一般来说，回归系数越高，预测越精确；反之，预测的误差越大。回归分析主要有：
❶一元线性回归。变量之间关系的数学表达式是一次函数，一次函数在坐标图上以直线表示，对这种关系的回归分析就是线性回归分析。只有一个自变量的线性回归叫一元线性回归。如根据学生智力测验的智商分数预测其学习成绩。
❷多元线性回归。自变量是两个或两个以上时的线性回归分析。其基本假定、原理及基本计算过程与一元线性回归是相同的。
❸曲线回归。有些变量之间关系的数学模型是曲线方程，由于按方程作出的曲线并没有一定的规律、趋势，因此，曲线回归一般用于描述而不用于预测，在心理学的实际研究中应用很少。

回归分析

数理统计的一个内容。详“相关分析”。

回归分析regression analysis

是两种现象或事物存在回归关系时，计算回归系数，并拟合出回归方程，对回归系数进行显著性检验，绘出回归线图。

回归分析Regression Analysis

用于揭示某一变量与另外一个或多个变量之间不确定性的数量关系的一种统计分析技术。一般而言，自然界各种现象之间存在两种关系：一种是确定性关系，可以用准确的数学函数来表达；另一种是不确定关系，即回归关系。回归分析的目的是揭示现象之间存在的不确定性关系式，分析某一变量的变动导致另外变量的可能变动的现象，来解释以上关系。按照涉及的自变量的多少，可分为一元回归分析和多元回归分析；按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析。如果在回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，该回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

回归分析

将经济变量之间的因果相关关系定量地描述出来的分析方法。参见“经济计量模型”。

回归分析

分析两个或多个变量之间相互关系的一种统计方法。回归这个名词是由英国生物学家高尔顿(F·Galton)首先提出来的。他在研究父亲身高与儿子身高之间的关系时发现，高个子父亲所生儿子比他更高的概率，要小于比他矮的概率； 同样，矮个子父亲所生儿子比他更矮的概率小于比他高的概率。这两端高度父辈的后代，其高度有向中心 （平均身高） 回归的趋势。生物统计学家把这种现象引用到统计预测上来，便形成了有名的回归分析方法。进行回归分析要首先建立变量之间的关系式，即回归方程式，然后通过回归方程式，由自变量的数值去测量变量的数值。回归分析中，一个因变量与一个自变量之间的回归称为简单回归或一元回归； 一个因变量与多个自变量之间的回归称为复回归或多元回归； 各变量值之间的数量关系在坐标系中能近似呈直线分布的称为线性回归或直线回归； 呈曲线分布的称曲线回归。因为回归分析的目的是要得到变量之间数量上的联系方程式及其变化规律，所以回归分析的用途很广，是分析因果变动和其他有联系变动的有力工具

回归分析

通过大量的观察数据寻求变量间相互依存的非确定性数量关系的一种统计技术。主要内容包括：
❶从观察数据出发，确定变量间的定量关系式，即确定出统计回归模型的具体形式和模型参数的估计值；
❷对所确定的估计进行统计检验，判断其显著性水平；
❸在所选择的诸因素中，判断相互影响的主要因素；
❹对客观过程进行分析、预测和控制，并给出其对精度的估计。回归方程可分作一元与多元，线性与非线性等。在人寿保险中预测未来业务的发展，探讨不同因素对保险效益的影响等，都能起到重要作用。

回归分析regression analysis

用于揭示某一变量与另外一个或多个变量之间的不确定性的数量关系的一种统计分析技术。一般而言，自然界各种现象之间存在两种关系，一种是确定性关系，可以用准确的数学函数来表达，另一种是不确定的关系，即所谓的回归关系。回归分析的目的就是揭示现象之间存在的不确定性关系式，分析某一变量的变动导致另外的变量的可能变动及其幅度。比如自然中存在某两个以Y和X测度的现象，来解释以上的两种关系。某一自变量X变动以后，因变量Y必然变动某一个数量，如：

Y=a+bX

所示，X变动一个单位，则Y必然变动b个单位，这种关系就是确定性关系，亦称为线性函数关系。
对于回归关系，以上面的Y和X为例，可以用如下的线性等式描述。

Y=a+bX+u

这里的u是一个随机变量，服从正态分布，均值为零，方差存在且有限。这里的回归方程反映的是不确定性关系，可以描述为X变动一个单位，Y平均变动b个单位，回归分析的结论是“可能”的，或者一般性的，不绝对，不肯定。对于上式，可以给出回归分析的基本思想：

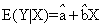
即Y在X给定时的条件期望为+X,、是a、b的估计值。
对于多元线性回归关系，有被解释变量向量Y和解释变量X，它们的观测值有n个，有下面用矩阵表达的回归方程式：

Y=XB+u

式中，X是解释变量矩阵，n行，p+1列；B是待估回归系数向量，已估参数用表示；u是随机扰动项；＝[X'X]^-1X'Y。
线性回归有以下几个重要假设：
❶Y服从多元正态分布；
❷E(Y)=XB;
❸cov(Y)=cov(Y)=σ²I。

回归分析Regression Analysis

是通过一定的相关关系的方程式从一个变量的变化去推断和预测另一个变量的变化值的资料分析方法。回归的概念最早是由英国的生物学家葛尔登提出的。后来由他的学生皮尔逊将回归同数学方法联系起来，把代表现象间的一般数学关系的直线（或曲线）叫做回归直线（或曲线）。而回归这个名词后来就被用来泛指变量之间的一般数量关系。在新闻传播研究中，使用相关系数虽然能够说明相关关系的密切程度和相关的方向，但却不能说明一个变量变化了，另一变量相应地发生了多大的变化。而回归分析则具有对变量之间数值变化的相互推测之功能。运用回归分析方法可以将较难测度的变量变成因变量，把较易测度的变量变成自变量，这样就可以用这种较易测度的变量去推测较难测度的变量。
应用回归分析必须是变量之间的相关关系非常密切，这样通过回归直线方程就能获得相当准确的推测值。用回归直线方程推算回归分析结果的准确程度的量度叫回归标准误差（估计标准误差），它能反映回归直线代表性的大小，具有和标准差同样的性质和作用，只不过标准差是说明平均数代表性的大小，回归标准差则是说明平均线代表性的大小。回归标准误差与相关系数的关系是：两者都具有说明相关关系密切程度的作用，只不过相关系数是用相对数表示，密切程度的概念较明确。而估计标准误差是用绝对数表示，对关系的密切程度表示不明显。同时估计标准误差不能说明相关关系是正相关和负相关。

回归分析Regression Analysis

处理变量之间相关关系的一种数理统计方法。变量的相关关系是多种多样的。当变量x为非随机变量，因变量Y是随机变量，对于自变量x的每一个确定的值，因变量Y有一个确定的概率公布与之相对应时，对这种相关关系的函数处理，叫做回归分析。运用回归分析法，需要先从变量的历史数据或实验数据统计资料中找出其内在联系，建立变量之间的经验公式（回归方程），再用自变量数值的变化去有效地预测因变量未来可能的取值范围。参见“回归预测”。

回归分析

研究现象变量之间相互依存关系的一种分析方法。就是利用统计和数学的方法，对客观经济现象中，某些变量之间，存在的相互依赖和某种不确定关系（称为相关关系），所进行的分析。在经济分析和研究中，它用于确定现象之间的定量关系，预测和控制某一变量的数值，分析影响某一变量值的主要和次要因素，作为经济管理决策的参考依据。其主要内容或步骤是：
❶找出影响被分析指标变化的主要因素，从观测数据出发，确定变量之间的定量关系的回归方程式。即y=a+bxε。式中x和y是具有线性相关关系的两个变量，x是自变量，y是因变量，a是常数，b是回归系数，ε是随机误差。
❷采用数学中曲线拟合的方法，根据样本资料计算各项参数的估计值。
❸根据参数估计，确定估计值的抽样误差和置信度。

回归分析regression analysis

用建立数学模型（即回归方程式）来反映变量之间联系规律，从而由自变量数值推测因变量数值的方法。设有因变量Y(Y亦可能是多个)，若对Y有影响的全部因素即自变量为X₁，…，X_r，即一般有关系式Y=f(X₁,X₂，…，X_r)。但由于种种限制，实际上只能考虑主要变量X₁，…，X_s,(S*(X₁+…+X_s)+e,e为随机误差。当X₁，…，X_s选定后，就需要估计f^*及误差e，由此求得的f^*称为Y对X₁，…，X_s的回归函数。对f^*在形状上不作规定的，为非参数回归；对f^*在形状上假定有一定的数学形式，其中有一些待定参数的，为参数回归。
参数回归中最重要的是线性回归，即f^*是若干未知参数β₁，…，β_p的线性函数：f^*(X₁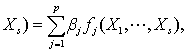，…，为已知函数。当对Y和X₁，…，X_s作n次试验，得n个方程：Y_i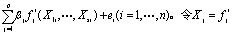＝(X₁，…，X_s)(j=1，…，p)，则有线性模型Y=Xβ+e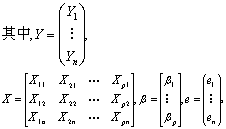

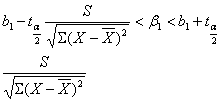
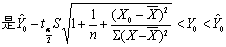
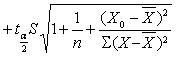随机误差e常被假定服从均值为0（误差无偏性）的正态分布，方差的齐性(D(e_i)=σ²)，及误差独立性(E(e_ie_j)=0)等。只有两个变量X,Y的简单线性模型为Y=β₀+β₁X+e，样本回归直线方程是y=b₀+b₁X,b₀、b₁分别是估计的截距与回归系数，其值由最小平方法确定。根据该方程可对X、Y的关系进行研究，并作预测分析。若置信度为1-α,β₁的置信区间是

S为剩余标准差。给定X₀，相应Y₀的预测区间当X、Y间呈非线性相关时，一定情况下可作适当的变量替换化为线性关系处理。在多元线性回归的情况下，可利用正交多项式计算，或用逐步回归等方法以追求最优回归方程。

回归分析

分析因变量与自变量之间的相互关系，选用合适的数学模式表述，从模式中一个或几个变量的数值去推算另一个变量的数值的分析方法。由于偶然因素的作用，变量与变量之间存在的关系不是确定性的。在研究变量间的关系时，把其中一些因素作为受控制的变量，即自变量，另一变量作为它们的因变量。回归一词由英国高尔顿 (F·Galton) 首先提出，他在研究生物血缘关系时发现，生物的后代有回归到历史原来性质的倾向。例如，特高的父亲所生的儿子，比父亲更高的概率要小于比父亲矮的概率；特矮父亲的儿子，比父亲更矮的概率要小于比父亲更高的概率。特高和特矮父辈的后代都有回归到人类平均身高的趋势。后来，把他采用的分析方法称为回归分析法。分析一个因变量和一个自变量的关系称为一元回归分析； 分析因变量和多个自变量之间的关系称为多元回归分析。因变量与自变量之间的关系是线性关系的，称为线性回归分析； 否则，称为非线性回归分析。

回归分析regression analysis

对具有相互联系的现象，根据其关系形式，择一合适的数学模式，用以近似地表达变量间平均变动关系的一种统计分析方法。由英国优生学家高尔顿(Galton,F.)首创。回归分析是研究两个或两个以上变量间关系形式，在分析研究时，不论研究的变量多少，应择其中之一，作为因变量，其余当作自变量。如果因变量与自变量的关系是线性的则称直线回归分析。反之，称曲线回归分析。研究一个因变量只与一个自变量的关系，就叫一元直线回归分析。其回归方程是最简单的，也是最常见的。其数学模式是：

y=a+bx

式中x为自变量，y为因变量，a为常数，b为回归系数。应用最小二乘法，求得a和b值和回归方程式，根据此式，在有效区间内，可以由x取值来预测y的值和估计误差。研究一个因变量和多个自变量的关系，就叫做多元直线回归分析，其模式为：

y=a+b₁x₁+b2x2+…+bnxn

式中a为常数，b₁,b₂，…b_n分别为y对x₁,x₂，…x_n的回归系数。在多元回归分析中，可采用最小二乘法一次回归，也可在研究的全部因素中，按其与y的相关程度大小，逐个把自变量引入模式，这就叫逐步回归。

回归分析regression analysis

在相关变量中将一个变量视为因变量，其他一个或多个变量视为自变量，建立回归模型并利用样本数据进行统计分析的统计方法。英国生物学家和统计学家高尔顿1889年首先发现回归现象，即向平均数方向的回归。主要用于分析变量之间的共变关系，确定变量间共变关系的数学模型，即回归模型，从而分析一个变量的变异在多大程度上可由其他变量的变异来解释和预测。被解释或预测的变量称因变量或回归变量，用于解释或预测的变量称自变量或预测变量。根据回归模型中自变量的数量可分为一元回归分析和多元回归分析。按照自变量和因变量间关系类型，可分为线性回归分析和非线性回归分析。若回归分析中，只包括一个自变量和一个因变量，且两者关系可用一条直线近似表示，这种回归分析称为“一元线性回归分析”；如果回归分析中包括两个或两个以上的自变量，且因变量和自变量间呈线性关系，则称为“多元线性回归分析”。回归分析基本过程为： 建立回归方程、检验方程有效性(包括方程本身有效性、方程中每个自变量的有效性)并确定有效性程度大小、在方程有效基础上利用回归方程进行预测和控制。

回归分析

在相关变量中将一个变量视为因变量，其他一个或多个变量视为自变量，建立回归模型并利用样本数据进行分析的统计分析方法。主要用于分析变量之间的共变关系，旨在确定变量间共变关系的数学模型，即回归模型，从而分析一个变量的变异在多大程度上可由其他变量的变异来解释和预测。被解释或预测的变量为因变量或回归变量，用于解释或预测的变量叫自变量或预测变量。根据回归模型中自变量的数量可分为一元回归分析和多元回归分析。回归分析的主要内容包含： (1) 回归方程的建立；(2) 检验回归方程的有效性；(3) 利用回归方程进行预测和控制。