四元数和八元数siyuanshu he bayuanshu

由实数的四元序对和八元序对分别构成的代数结构.复数可以看成是实数的二元序对构成的代数结构.英国数学家哈密尔顿首先引入四元数系，这是在放弃乘法适合交换律，保留其他算律而得到的超复数系.
令S = {(a,b,c,d) |a,b,c,d∈R}，即实数四元数组的集合.并规定

则可证明加法适合交换律、结合律，(0,0,0,0)是零元，即(0,0,0,0)+(a,b,c,d)=(a,b,c,d)；乘法适合结合律，且有单位元(1,0,0,0)，即对一切(a,b,c,d)有(1,0,0,0)·(a,b,c,d)=(a,b,c,d)；乘法对加法适合分配律；并且，当(a,b,c,d)≠0时.

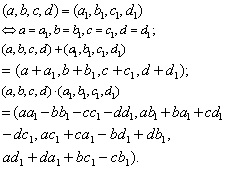
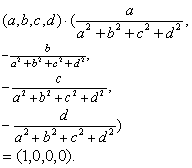
但一般地，αβ≠βα.
这样，S联同加法、乘法做成的系统称为四元数系.这是一个超复数系，其元素称为四元数.
四元数理论在理论力学中得到一些应用.但四元数在其他方面的尝试并未成功，它的作用与复数的作用是不能比的.
若令1=(1,0,0,0),i=(0,1,0,0),j=(0,0,1,0),k=(0,0,0,1)，则(a,b,c,d)=a+bi+cj+dk).a称为它的实数部分，bi+cj+dk)称为它的向量部分.
设a=a+bi+cj+dk，令a^*＝a-bi-cj-dk称为a的共轭.容易证明，a·a*=a²+b²+c²+d²；并且(αβ)^*＝β^*α^*.
在探讨超复数系的过程中，还提出了拟四元数的概念以及八元数的概念.由于，这种系统与普通数系差别太大，又没有找到应用，在数学史上没有多大影响.最著名的是凯莱提出的八元数概念.
八元数定义为由二个四元数的序对(a,b)所组成.其运算为

(a,b)+(c,d)=(a+c,b+a),

(a,b)(c,d)=(ac-d^*b,da+bc*),a(a,b)=(aa,ab),a∈R

其中c^*,d^*分别为四元数c,d的共轭.若令1=(1,0),e₁＝(i,0),e₂＝(j,0),e₃＝(k,0),e₄＝(i,0),e₅＝(0.i),e⁶＝(0,j),e⁷＝(0,k)，则有乘法表

	1	e1	e2	e3	e4	e5	e6	e7
1	1	e1	e2	e3	e4	e5	e6	e7
e1	e1	— 1	e3	— e2	e5	—e4	—e7	e6
e2	e2	— e3	— 1	e1	e6	e7	—e4	—e5
e3	e3	e2	— e1	— 1	e7	— e6	e5	—e4
e4	e4	— e5	— e6	— e7	— 1	e1	e2	e3
e5	e5	e4	— e7	e6	— e1	— 1	— e3	e2
e6	e6	e7	e4	— e5	—e2	e3	—1	—e1
e7	e7	—e6	e5	e4	— e3	— e2	e1	—1

每个八元数可写成

x=x₀+x₁e₁+…+x₇e₇,x₁∈R

八元数乘法不满足交换律和结合律，如

e3(e4e5) ≠

(e3e4)e5

；但满足yx²＝(yx)x,x²y=x(xy).
1861年，威尔斯特拉斯证明(1864年发表):保存普通数系所有性质不变(即满足加法交换律、结合律；乘法结合律、交换律，且乘法对加法分配律)，要构造比复数系更一般的数系是不可能的.而1878年佛罗贝尼乌斯证明：满足除去乘法交换律以外所有代数基本性质的超复数系，只有四元数一种.至此，对于数系的讨论圆满地完成了.