可重复的排列
可重复的排列ke chongfu de pailie
从n个不同的元素里,每次取出m个元素,元素可以重复出现,按照一定的顺序排成一排,叫做从n个不同元素里每次取出m个元素的可重复排列。由于第一、第二、………、第m位上选取元素的方法都是n个。因此,从n个不同的元素里,每次取出m个元素的可重复排列的种数是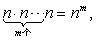 用符号记作Rnm =nm,也可以记作
用符号记作Rnm =nm,也可以记作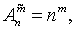 特殊地,
特殊地,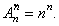
可重复的排列的模型为:设有带号码1,2,………,n的n种球,每种有足够多个,多于抽取个数(此即可重复性)。在这堆球中依次取出m个(m可以比n大),把这m个号码按抽取的先后次序排成一排,则其不同排法的数目,记作Rnm=nm。
用集合语言可表述如下:
设集合A={a1,a2,………,an},则直积集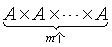 叫做从n个元素中每次取出m个元素的可重复排列集,其元素的个数叫做可重复的排列数,记作Rnm,其中每个元素(m重序)叫做一个可重复的排列。其中m
叫做从n个元素中每次取出m个元素的可重复排列集,其元素的个数叫做可重复的排列数,记作Rnm,其中每个元素(m重序)叫做一个可重复的排列。其中m
根据以上定义,可得到如下定理:从集合A={a1,a2,………,an}中的n个元素里,每次取出m个元素的可重复排列数为Rnm=nm。
在解这方面的实际问题时,不必硬套公式,只要利用乘法原理分析问题,即可把问题解答出来。
比如,有三封不同的信,投入4个信箱里,共有多少种投信的方法?
这个问题可以从两种不同角度出发考虑: 一是可以从把信投入信箱里考虑(以信为主);二是可以从信箱里收到信考虑 (以信箱为主)。若以信为主考虑,则第一封信有四种不同的投法,不论把它投入哪个信箱里,第二封信还有四种投法。同理,第三封信也有四种投法。根据乘法原理,共有4×4×4=43=64种投信方法。
若以信箱为主考虑,则第一个信箱里会出现没有收到信,收到一封信,收到二封信,收到三封信等情况,所以共有 (C30+C31+C32+C33)种方法。这时,第二个信箱里的情况就非常复杂了,因此,循此思路很难计算出结果。若遇到这类情况,就应变换角度去考虑问题。
又如,有数、理、化三个课外小组,5个同学报名,每人限报一个组,共有多少种报名方法?
第一个同学有3种报名方法,不论他报了哪一个组后,第二个同学还有3种报名方法,其余类推,共有35=243种报名方法。
此处,若以小组为主出发考虑,则会遇到类似上例的情况,故不宜循此去解决问题。
☚ 组合数 可重复的组合 ☛
- r2022090420000428是什么意思
- r2022090420000429是什么意思
- r2022090420000431是什么意思
- r2022090420000432是什么意思
- r2022090420000433是什么意思
- r2022090420000435是什么意思
- r2022090420000436是什么意思
- r2022090420000437是什么意思
- r2022090420000438是什么意思
- r2022090420000439是什么意思
- r2022090420000440是什么意思
- r2022090420000441是什么意思
- r2022090420000443是什么意思
- r2022090420000444是什么意思
- r2022090420000445是什么意思
- r2022090420000446是什么意思
- r2022090420000448是什么意思
- r2022090420000449是什么意思
- r2022090420000450是什么意思
- r2022090420000452是什么意思
- r2022090420000454是什么意思
- r2022090420000455是什么意思
- r2022090420000456是什么意思
- r2022090420000457是什么意思
- r2022090420000458是什么意思
- r2022090420000460是什么意思
- r2022090420000461是什么意思
- r2022090420000463是什么意思
- r2022090420000464是什么意思
- r2022090420000465是什么意思
- r2022090420000466是什么意思
- r2022090420000467是什么意思
- r2022090420000469是什么意思
- r2022090420000470是什么意思
- r2022090420000471是什么意思
- r2022090420000473是什么意思
- r2022090420000474是什么意思
- r2022090420000476是什么意思
- r2022090420000477是什么意思
- r2022090420000478是什么意思
- r2022090420000479是什么意思
- r2022090420000480是什么意思
- r2022090420000482是什么意思
- r2022090420000483是什么意思
- r2022090420000484是什么意思
- r2022090420000485是什么意思
- r2022090420000487是什么意思
- r2022090420000488是什么意思
- r2022090420000489是什么意思
- r2022090420000491是什么意思
- r2022090420000492是什么意思
- r2022090420000493是什么意思
- r2022090420000494是什么意思
- r2022090420000495是什么意思
- r2022090420000496是什么意思
- r2022090420000497是什么意思
- r2022090420000498是什么意思
- r2022090420000499是什么意思
- r2022090420000501是什么意思
- r2022090420000502是什么意思