可数集keshuji

设N是自然数集，如果集合A与N等价，即A～N，那么就称A是可数的.也就是说，一切同N等价的集合都是可数集.
由于自然数的特点是可以从它的最小数1开始，从小到大一个个排列起来，只要知道前一个数，就可以说出下一个数，虽然数不尽，但我们总是可以一直数下去，这就是“可数集”称谓的来由.
由可数集的定义可以得到，一个无限集合A是可数集的充要条件是：A可以写成序列形式

A={a₁,a2，…，an，…}.

例如，设是非负有理数集，可以用下面的方法把非负有理数排列出来

非负整数	0, ↙	1, ↙	2, ↙	3, ↙	4,	……
分母是2的正有理数	1/2, ↙	3/2, ↙	5/2, ↙	7/2,	9/2,	……
分母是3的正有理数	1/3, ↙	2/3, ↙	4/3,	5/3,	7/3	……
分母是4的正有理数	1/4, ↙	3/4,	5/4,	7/4,	9/4,	……
分母是5的正有理数	1/5,	2/5,	3/5,	4/5,	6/5,	……
……	……

按照上表中“↙”的顺序把这些数都排列起来就是：

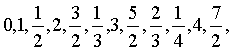
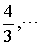
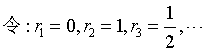
则非负有理数集

可写成

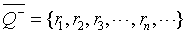
的序列形式.可见是一个可数集.
用同样的方法可以证明负有理数集Q-是一个可数集；全体有理数集Q=∪Q-是可数集.
可数集有以下性质：
❶可数集的任何无限子集仍是可数的；

❷任意可数集A与有限集B的并集A∪B是可数集；

❸任意两个可数集A和B的并集A∪B是可数集；
此性质可推广为：任意n个可数集A₁,A₂，…，A_n的并集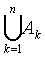是可数集.当n→∞时，并集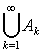仍是可数的；

❹任意一个可数集A与有限集B的笛卡儿积A×B是可数集；

❺任意两个可数集A和B的笛卡儿积A×B是可数集；

❻任意n个可数集A₁,A₂，…，An的笛卡儿积A₁×A₂×A₃×…×A_n是可数集.