可导性与连续性的关系kedaoxing yu lianxuxin g deguanxi

若函数f(x)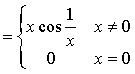在点x₀可导，则f (x) 在点x₀连续. 反之不真。
例如，函数 虽然在点x=0连续，但在这一点不可导。
函数f (x)在连续点不可导的类型有
❶ 左、右导数都存在，但不相等。

❷ 左、右导数中至少有一个不存在，但不是无穷大量。

❸ 左、右导数中至少有一个是无穷大量。
微分学自17世纪末建立后，虽然发展很快，但在相当长的时间内，函数的可导性与连续性的关系问题没有得到解决。不少数学家想证明，区间上的连续函数只在个别点上不可导。1861年，维尔斯特拉斯作出了第一个在任何点上都不可导的连续函数的例子 (发表于1875年)，从而解决了可导性与连续性的关系问题。这个例子是：

这里0 1 +3π/2。

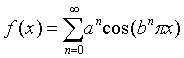
☚ 左导数和右导数 　 导数的四则运算法则 ☛