变换的乘积bianhuan de chengji

是一种变换，相当于连续进行两次变换.在平面或空间的任意两个一一变换F₁,F₂，对点A先进行第一个变换F₁，这时点A变为点A₁，即F₁(A)→A₁；接着进行第二个变换F₂，这时，点A₁变为点A₂，即F₂(A₁)→A₂，这样连续进行F₁,F₂两个变换，把点A变为点A₂的过程，叫做两个变换F₁,F₂的乘法，记作F₂·F₁.
能够验证，连续进行两个变换后，结果仍是一个变换，这个变换就是前两个变换的乘积.设变换的乘积为F，前两个变换为F₁,F₂，则有F=F₂·F₁.
类似地可以定义有限个变换的乘法和变换的乘积.

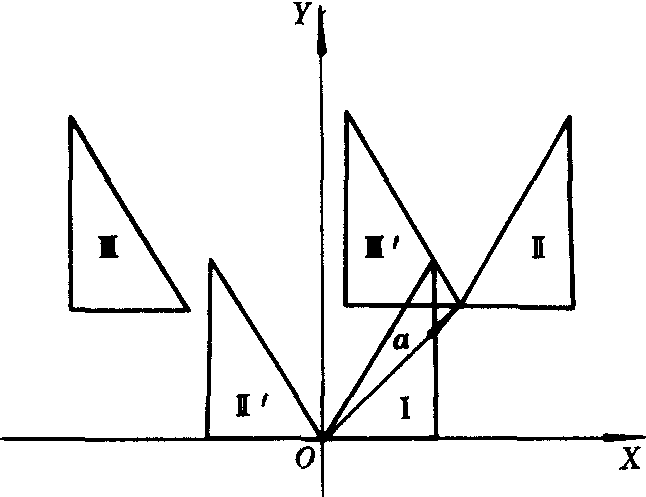
例如，如图，F₁是一个沿a的方向和大小移动的平移变换，F₂是一个关于Y轴的对称变换，则经过F₂·F₁，图形Ⅰ变到了图形Ⅱ，又变到了图形Ⅲ.把图形Ⅰ变到图形Ⅲ的变换F，就是F₁和F₂的乘积，即F=F₂·F₁.
在一般情况下，变换的乘法不满足交换律，即F₂·F₁≠F₁·F₂.如图，先进行变换F₂，图形Ⅰ变为图形Ⅱ′，再进行变换F₁，把图形Ⅱ′变为图形Ⅲ′，显然F₂·F₁≠F₁·F₂.特殊情况下，如两个平移变换的乘积仍是平移变换，而且交换变换的顺序，乘积不变.